Note 3 Shading

文章目录

1. 1. יְהִי אוֹר
   1. 1.1. 漫反射（Diffuse Reflection）
   2. 1.2. 镜面反射（Specular Reflection）
   3. 1.3. 环境光（Ambient Lighting）
   4. 1.4. 冯氏光照模型
2. 2. UV映射
3. 3. 着色方法
   1. 3.1. 平面着色（Flat Shading）
   2. 3.2. 逐顶点着色（Gouraud Shading）
   3. 3.3. 逐像素着色（Phong Shading）
4. 4. 渲染管线
5. 5. 纹理放大和纹理缩小
   1. 5.1. 纹理放大
   2. 5.2. 纹理缩小
6. 6. 其他小知识

יְהִי אוֹר

起初，计算机的世界尚未渲染，显示器中空虚混沌，渊面黑暗。

唯有顶点与多边形悬于虚空，不见其形，不辨其色。

那声音说：“要有光。”

就有了光。

光是好的，于是那声音将光与暗分开了。光所照之处，物体的正面得以显现；光所不至的背面，则归于阴影。从此，三维的世界有了明暗与层次。

这光并非一体。

那普照万物，均匀散开，使物体显其本色的，称之为漫反射。

那汇于一点，锐利夺目，使光滑之物尽显其耀的，称之为镜面反射。

那弥漫于环境，充盈于阴影，使黑暗不至完全吞噬一切的，称之为环境光。

有漫反射，有镜面反射，有环境光，共同构成了这虚拟世界的第一个白昼。

漫反射（Diffuse Reflection）

在漫反射中，光向四面八方散去，所以物体漫反射出的光与摄像机位置无关，而仅与以下几项有关：

1. 光强 $c_l$.
2. 物体材质 $c_r$. 不同物体对光的反射率是不同的，即使是同一个物体也对不同颜色的光有不同反射率。
3. 物体表面法线 $\bold{n}$.
4. 光源方向 $\bold{l}$.

最终结果可以写成

$$L_d = c_r c_l \max (0, \bold{n} \cdot \bold{l})$$

由于光强一般随距离衰减，所以 $c_l$ 一般反比于距离的平方 $r^2$.

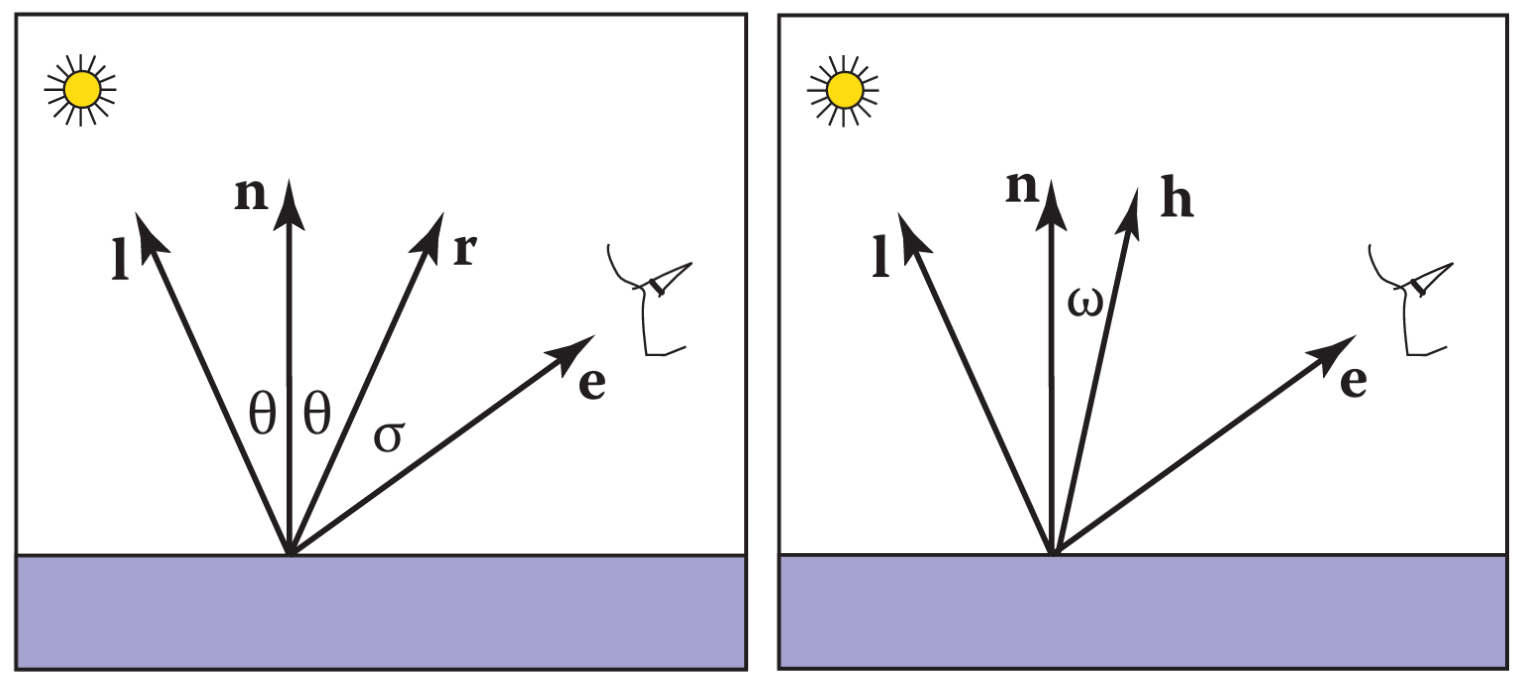
镜面反射（Specular Reflection）

镜面反射中，光主要向一个方向反射，所以镜面反射的光与摄像机位置有关。

$$L_s = c_pc_l\max(0, \bold n \cdot \bold h)^p$$

其中 $c_p$ 是自定义的 RGB 值，允许我们控制高光颜色，指数 $p$ 是为了保证我们只在小范围内看到高光，$p$ 越大这个高光可见范围越小，而 $\bold h$ 的定义如下：

$$\bold h = (\bold e + \bold l).\text{normalized()}$$

还有一种写法把 $\bold n \cdot \bold h$ 换成了 $\bold r \cdot \bold e$，简单计算可以发现 $\bold
n$ 和 $\bold h$ 的夹角是 $\bold r$ 和 $\bold e$ 的夹角的一半，所以这两个写法在思路上是一样的，都在考虑反射光方向和摄像机方向的夹角，不过在数值上会略有差别。本文采用 $\bold n \cdot \bold h$ 的写法。

环境光（Ambient Lighting）

如果只考虑漫反射和镜面反射，我们会发现没有面朝光源的物体完全是黑色的，但现实里显然不是如此。这是因为在现实里，光经过多次反射而照亮了那些没有面朝光源的物体。我们可以近似地认为有一种充斥着整个空间的光，并把它叫做环境光，公式如下：

$$L_a=c_r c_a$$

其中 $c_a$ 是环境光的强度。

冯氏光照模型

综合来看，我们就得到了冯氏光照模型，公式如下：

$$L=c_r(c_a+c_l\max{(0,\bold n \cdot \bold l)})+c_pc_l\max(0, \bold n \cdot \bold h)^p$$

其中

1. $c_r$ 是物体材质，表示物体对光的反射率，一般是一个 Vector3f 类型的值，因为物体对不同颜色的光有不同反射率；
2. $c_a$ 是环境光强，一般是一个 Vector3f 类型的值；
3. $c_l$ 是光强，一般与物体和光源的距离成反比，一般是一个 Vector3f 类型的值；
4. $c_p$ 是高光颜色，一般也是一个 Vector3f 类型的值。

UV映射

为了把贴图贴到模型上，需要有一个 $(x, y, z) \rightarrow (u, v)$ 的函数 $\phi$. 我们期望这个函数有这些性质：

1. 单射：我们不希望两个 3D 点映射到同一个 2D 点上
2. 大小不变性：在 3D 模型上的三角形多大，我们希望 2D 的三角形也差不多大小
3. 形状不变性：3D 模型的三角形映射到 2D 上后，两个三角形应尽量相似
4. 连续：如果两个点在 3D 世界模型上相近，我们希望它们在 2D 上也相近

贴图有许多应用，最容易想到的是颜色贴图，它直接把颜色贴到模型上，也被称作漫反射贴图。

法线贴图、金属度贴图、粗糙度贴图则进一步决定了模型的各种属性。比如法线贴图定义了每一点的法线，在计算光照时会借助这个法线来得到更真实的结果。

着色方法

模型由三角形划分来表示，那么每个三角形用怎样的颜色呢？

平面着色（Flat Shading）

我们通过光照计算颜色，而计算光照需要法线。平面着色直接求这个三角形的法线，然后按光照公式计算这个三角形的颜色。这种方法得到的每个三角形都是单色的。

逐顶点着色（Gouraud Shading）

逐顶点着色则求三角形顶点的法线，并为三角形顶点着色，然后对内部的每个点插值内部颜色。

那么顶点的法线是什么呢？一个顶点一般在多个面上，把这些面的法线做加权平均就好，权值可以是面的面积。

逐像素着色（Phong Shading）

逐像素着色同样求三角形顶点的法线，然后对内部的每个点插值内部法线，从法线再求各个点的颜色。

插值是通过重心坐标来插值。对三角形 $ABC$ 内的某一点 $P$，它可以表示为

$$P=\frac{S_{APB}C+S_{BPC}A+S_{CPA}B}{S_{ABC}}$$

这里的 $S$ 是面积，这里的形如 $S{APB}/S{ABC}$ 的式子就是各个点的权值。

在插值时，我们希望在世界空间 / 摄像机空间做插值，即在 viewing transformation 前进行插值，而不是 viewing transformation 后。

但我们一般在光栅化时才进行插值，这时已经把物体变换到了 NDC 空间，所以我们还要进行透视矫正。公式如下，具体推导可以参考 Homework 3 的笔记。

$$\begin{align*} &\alpha = \frac{\alpha' / w_0}{\alpha' / w_0 + \beta' / w_1 + \gamma' / w_2} \\ &\beta= \frac{\beta' / w_1}{\alpha' / w_0 + \beta' / w_1 + \gamma' / w_2} \\ &\gamma= \frac{\gamma' / w_2}{\alpha' / w_0 + \beta' / w_1 + \gamma' / w_2} \end{align*}$$

其中 $\alpha’,\beta’,\gamma’$ 是屏幕空间的重心坐标，$\alpha,\beta,\gamma$ 是世界空间的重心坐标。我们用世界空间的重心坐标作为权重来插值。

渲染管线

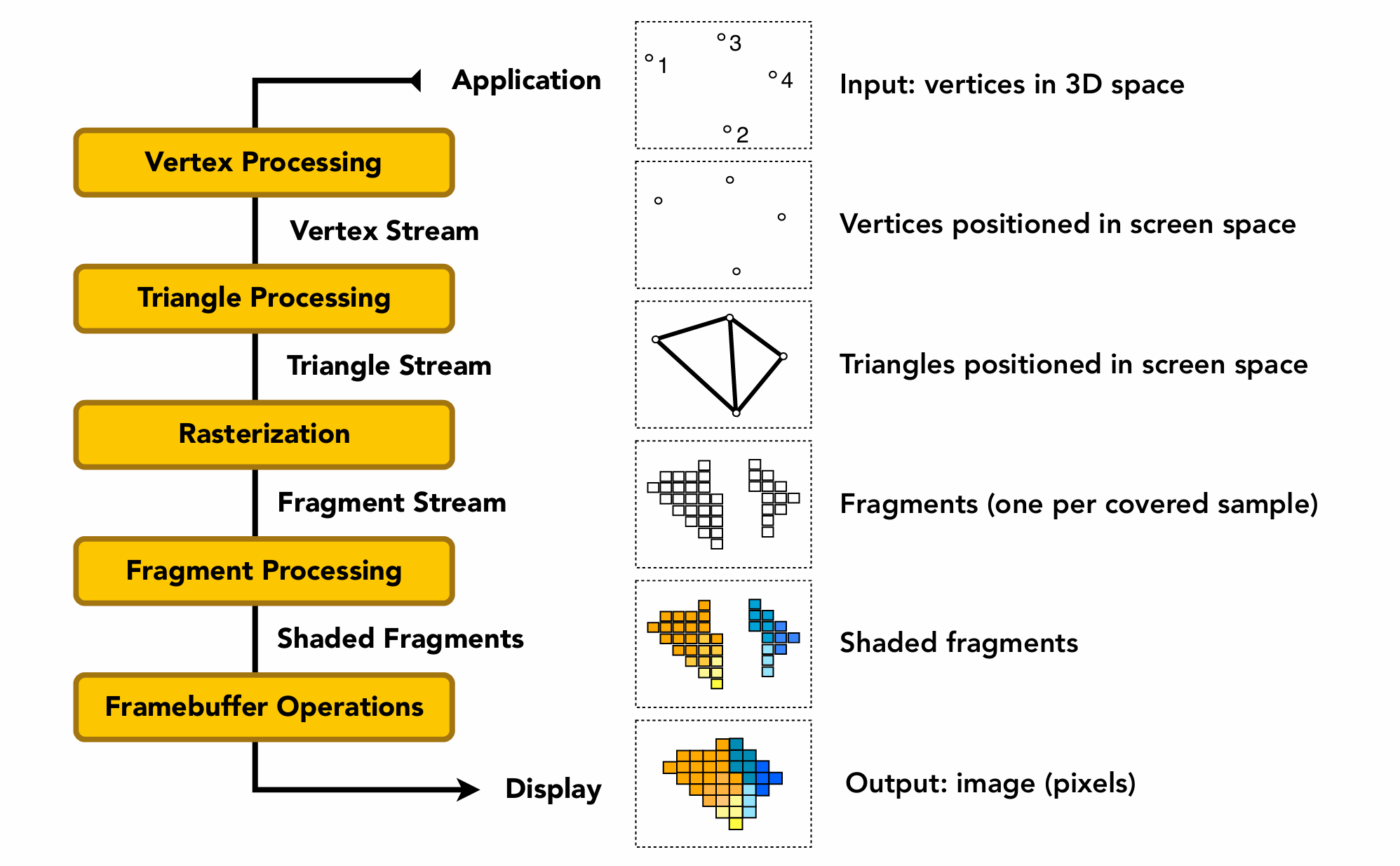
渲染流程基本如下：

1. Input：输入 3D 世界的顶点
2. Vertex Processing：用各种变换矩阵把顶点变换到屏幕空间
3. Triangle Processing：根据传入的顶点连接方式在屏幕空间连接三角形
4. Rasterization：把三角形转化成片元 / 像素
5. Fragement Processing：应用贴图、光照等
6. Framebuffer Operations：深度测试等

纹理放大和纹理缩小

在做纹理映射时，帖图太小和贴图太大都会有问题。

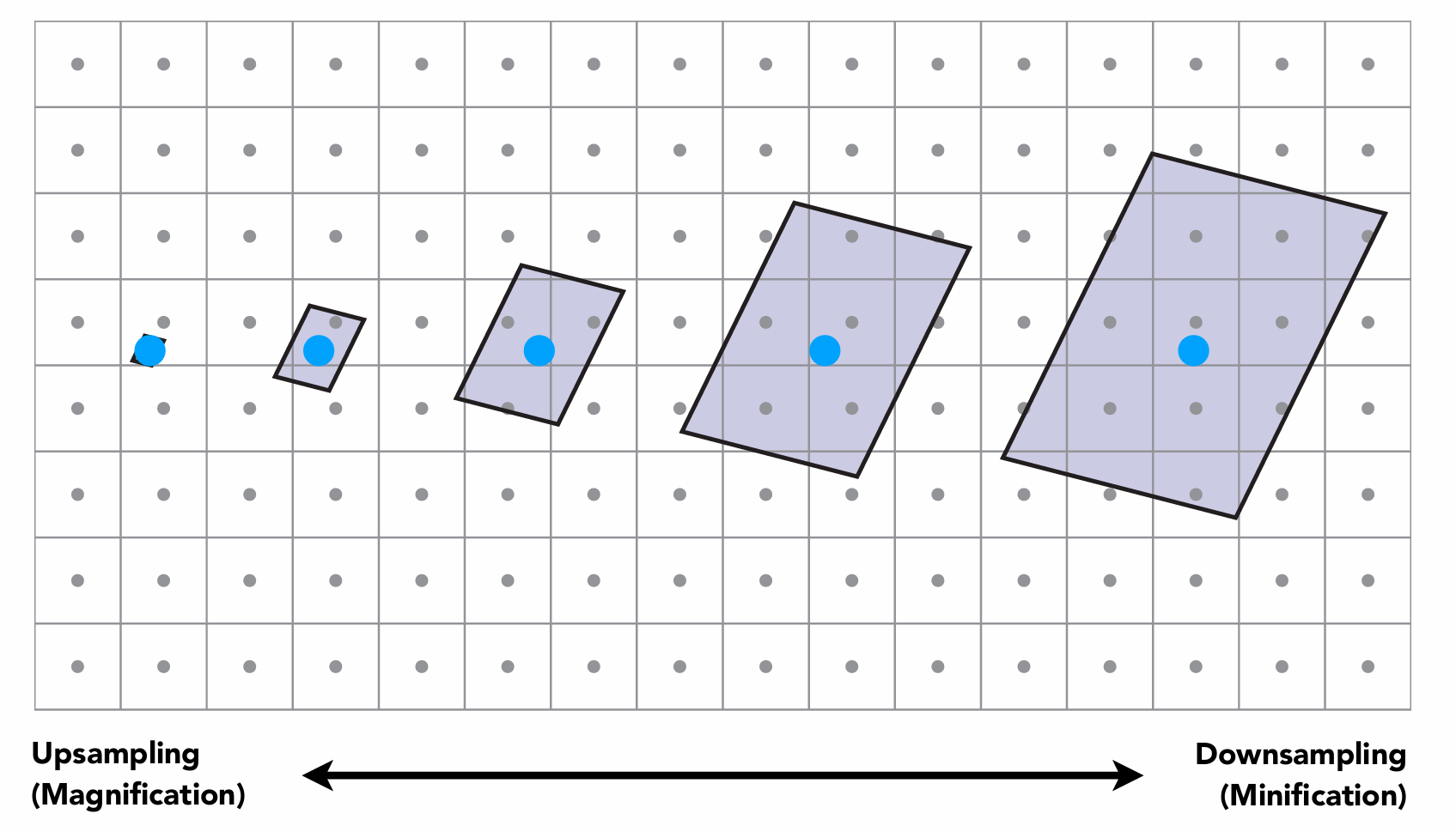
纹理放大

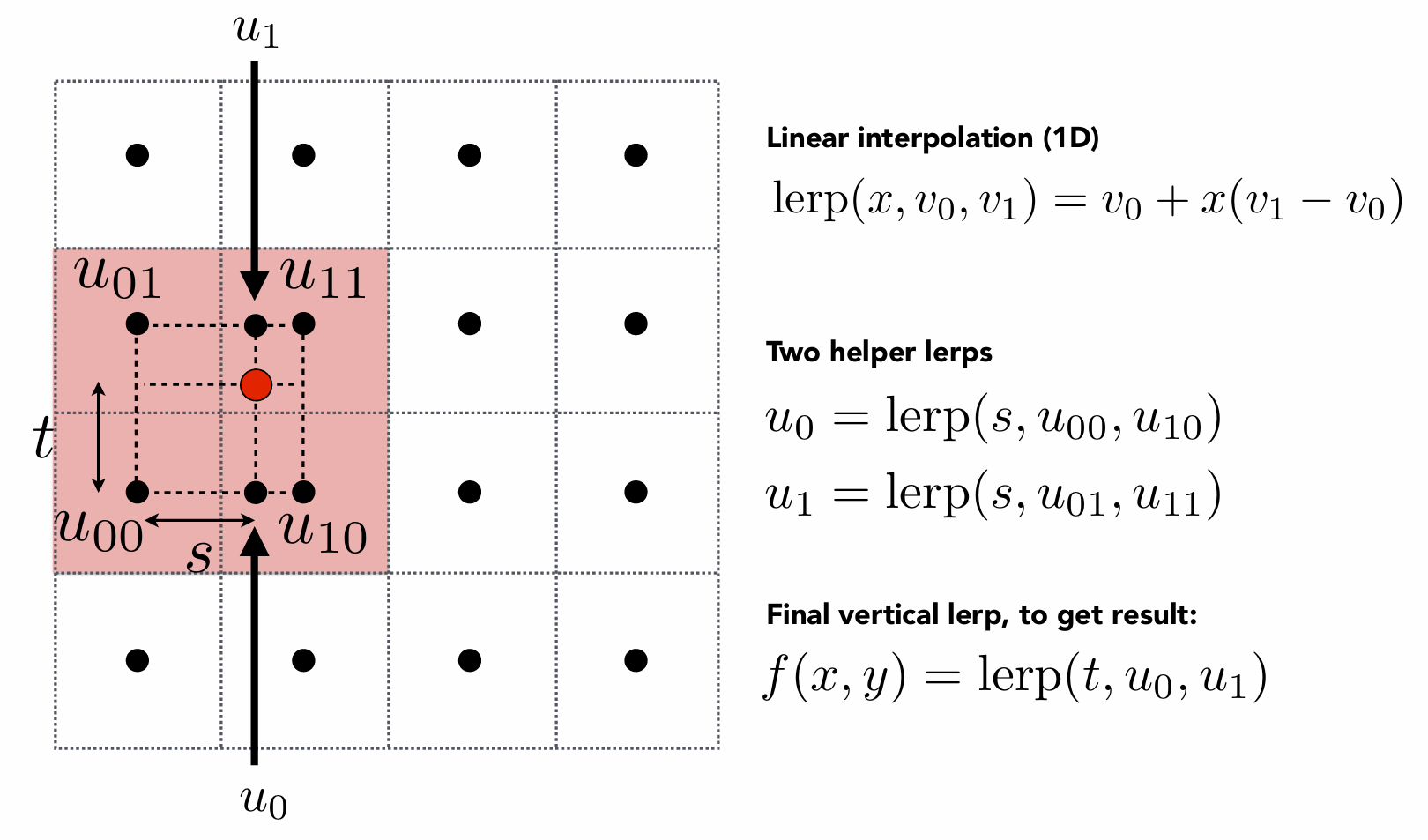
贴图太小时要做纹理放大，对采样点做双线性插值即可。

纹理缩小

贴图太大时直觉上比帖图太小更好处理，但恰恰相反。还记得频谱吗，帖图太大代表高频有更多信息，我们会因采样频率不足而无法正确反映高频信息，导致结果出现锯齿、摩尔纹等走样问题。

最常用的缓解方法是 Mipmapping。基本思路是，我们分析屏幕上每个像素在贴图上覆盖的像素数量，对那些覆盖较多的，就让他们去被缩小的贴图上采样，这样就能缓解欠采样问题。

首先我们要创建“缩小的贴图”，Mipmap链包含一系列纹理 $D_0, D_1, D_2, \ldots, D_N$，其中 $D_i$ 的分辨率为 $\frac{W}{2^i} \times \frac{H}{2^i}$，直到最内层为 $1 \times 1$ 像素。

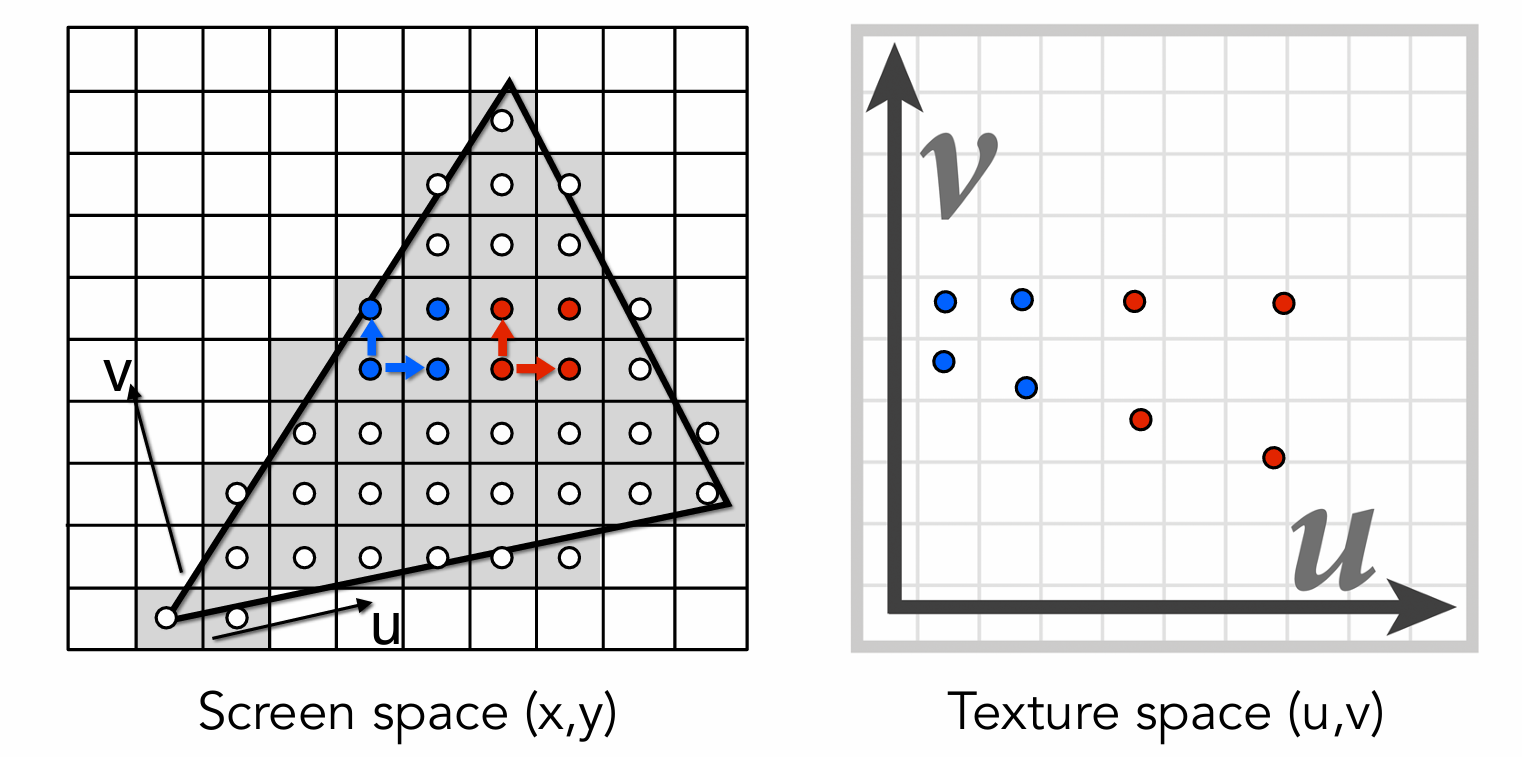
然后我们要分析单个屏幕像素覆盖了多少纹理像素，大致思路是计算屏幕空间的相邻点映射到贴图空间后的距离。贴图空间里相邻像素距离为 $1$，所以如果屏幕空间的相邻点映射到贴图空间后的距离为 $x$，我们就认为它覆盖了 $x$ 个像素。

这个“单个屏幕像素覆盖了多少纹理像素”的估算被记作 $\rho$，公式如下：

$$\rho = \max\left( \sqrt{\left(\frac{\partial u}{\partial x}\right)^2 + \left(\frac{\partial v}{\partial x}\right)^2}, \sqrt{\left(\frac{\partial u}{\partial y}\right)^2 + \left(\frac{\partial v}{\partial y}\right)^2} \right)$$

取 $\max$ 是为了尽可能取层级更低的 Mipmap。一个屏幕像素覆盖的纹理像素越多，它对应的 Mipmap 层级就越小。总之，我们宁可模糊，也不要欠采样。

最后用 $\lambda = \log_2{\rho}$ 就能算出这个屏幕像素对应的纹理层级。比如当 $\lambda = 0$ 时，表示一个屏幕像素恰好对应一个纹理像素，应使用原始纹理 $D_0$.

计算出层级 $\lambda$ 后还要做采样。显然 $\lambda$ 大多数时候都不是整数，所以有两种常见的采样方法：

1. 最近邻Mipmap滤波（Nearest Mipmap Filtering）

   选择最接近 $\lambda$ 的整数层级 $d = \text{round}(\lambda)$ 做采样，在这一层可以是最近邻或双线性滤波。

2. 三线性滤波（Trilinear Filtering）

   确定 $\lambda$ 两侧的两个整数层级：$d_1 = \lfloor\lambda\rfloor$ 和 $d_2 = \lceil\lambda\rceil = d_1 + 1$，在这两层分别做双线性滤波采样得到颜色 $C_1$ 和 $C_2$，然后得到最终颜色

   $$C = (1 - f) \cdot C_1 + f \cdot C_2$$

   其中 $f = \lambda - \lfloor\lambda\rfloor$ 为 $\lambda$ 的小数部分。

其他小知识

虎书提到的planar projection、spherical coordinates、cylindrical coordinates、cubemaps本质上都是把3d表面投影到一个理想的简单几何体上，然后把简单几何体展开成平面。