Note 2 Rasterizing

文章目录

1. 1. Z-Buffer
2. 2. 走样现象
3. 3. 数学知识
   1. 3.1. 卷积
   2. 3.2. 傅里叶级数和傅里叶变换
   3. 3.3. 傅里叶变换的性质
   4. 3.4. 狄拉克脉冲函数和冲激串
   5. 3.5. 卷积定理
4. 4. 走样的原因
5. 5. 滤波器和走样的缓解方法
6. 6. 其他小知识
   1. 6.1. 常见滤波器的傅里叶变换
   2. 6.2. 卷积的单位元
   3. 6.3. 二维卷积和二维滤波器
   4. 6.4. 伽马值
   5. 6.5. 图像锐化
   6. 6.6. 图像缩放

在 Transformation 部分，我们已经可以把一个三维空间里的三角形投影到平面上。但怎么把一个纯色三角形绘制到屏幕上呢？我们知道屏幕由大量的像素点组成，那么怎么确定每个像素点是什么颜色呢？

我们通过采样给每个像素点涂上颜色。我们可以检查每个像素的中心点是否在这个三角形内部，如果在则涂上三角形的颜色。虽然这样绘制的三角形会有锯齿，效果一般，但基本思想就是这样。

那么如果有多个三角形，而且他们之间有遮挡关系呢？这就需要 Z-Buffer 出场了。

Z-Buffer

Z-Buffer 的算法如下面的伪代码所示。思路是对每个像素所在的所有三角形，取 z 值最小的三角形的颜色作为这个像素的颜色。

foreach (Triangle triangle in triangles) {
    foreach (Vector3 sample in triangle.GetSamples()) {
        // z 值越小显示越靠前
        if (sample.z < zBuffer[sample.x, sample.y]) {
            frameBuffer[sample.x, sample.y] = sample.rgb;
            zBuffer[sample.x, sample.y] = sample.z;
        }
    }
}

这也有良好的并行性，因为三角形的遍历顺序和最终结果无关，像素的绘制顺序也和最终结果无关。

虎书还提到我们会将 $z$ 值映射到 $[0, B-1]$，用整数存储 $z$ 值，但其实这是现在不再使用的方法，我们现在通常使用 24 位或 32 位的浮点数来存储深度值。（怪不得我查了好久资料都没查到“整数映射”的具体代码，原来早就不用了！！！）

走样现象

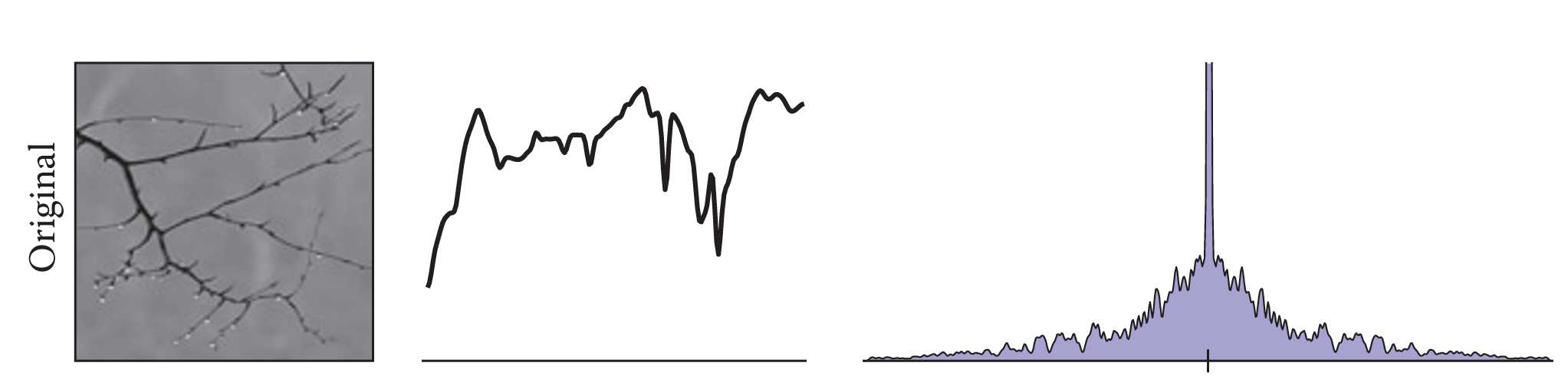
我们之前说过，简单的采样会出现锯齿，如下图所示。

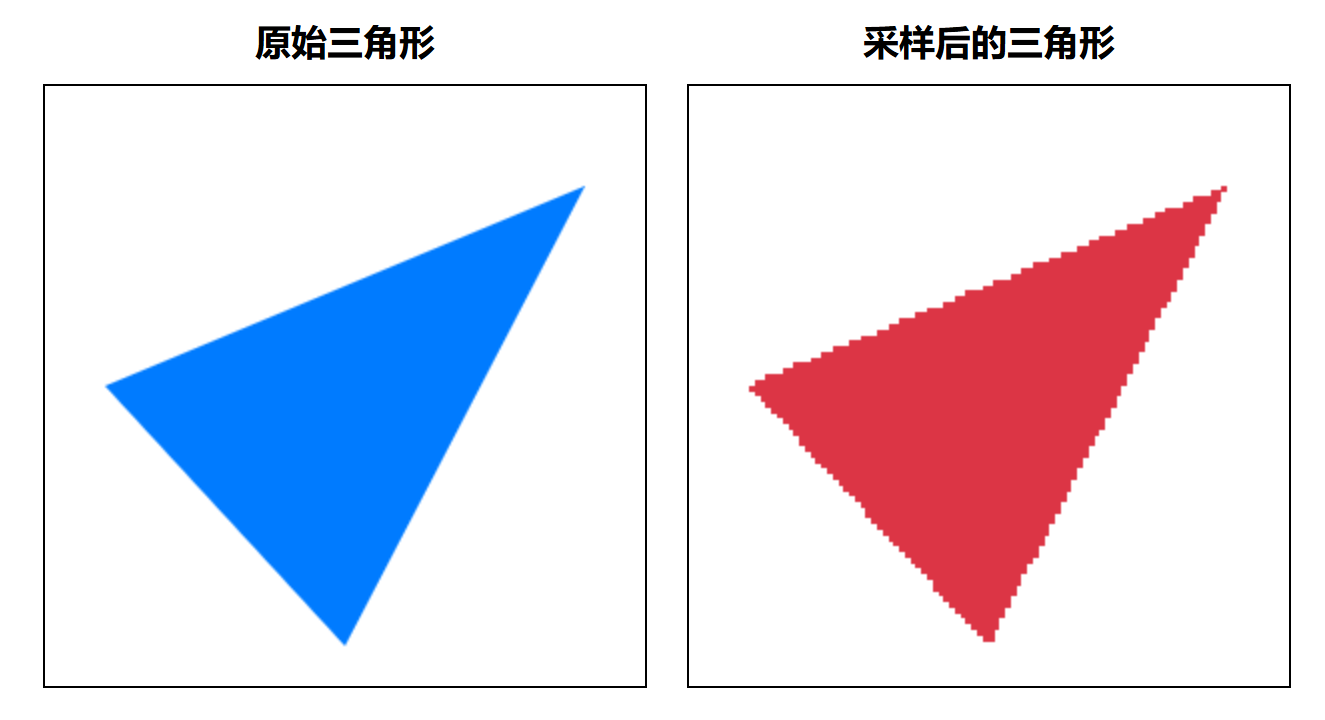
锯齿、摩尔纹之类的采样图像与原图不符的现象被统称为走样（Aliasing）现象，走样的实质是原图的高频信号被错误采样。为了明确什么是”高频信号”并找到缓解走样现象的方法，我们先看看一些数学知识。

数学知识

为了不让文章太长，这里我们省略所有的证明。不过所有的证明都并不困难，有空的话可以自己证一下试试。

卷积

我们先来看看三种卷积——离散-离散卷积、连续-连续卷积、离散-连续卷积。下面的 $f_{\rightarrow t}$ 表示将函数 $f$ 向右平移 $t$ 长度得到的新函数：

离散-离散卷积

$$\begin{align*} &(a*b)[i]= \sum_{j}a[j]b[i-j] \\ &(a*b)=\sum_{j}a[j]b_{\rightarrow j} \end{align*}$$

连续-连续卷积

$$\begin{align*} &(f*g)(x)=\int_{-\infty}^{\infty} f(t)g(x-t)dt \\ &(f*g)=\int_{-\infty}^{\infty} f(t)g_{\rightarrow t}dt \end{align*}$$

离散-连续卷积

$$\begin{align*} &(a*f)(x)=\sum_{i}a[i] f(x-i) \\ &(a*f)=\sum_{i}a[i]f_{\rightarrow i} \end{align*}$$

我们会注意到，卷积可以表示为函数平移后的加权和。

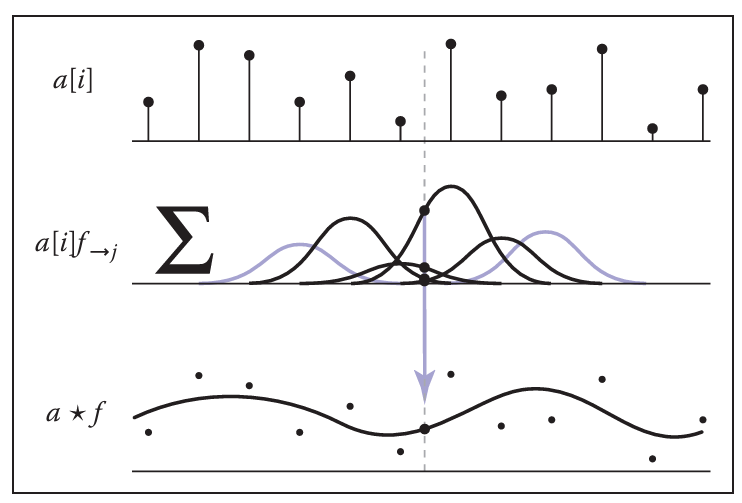
卷积是过会儿会用到的妙妙小工具。

傅里叶级数和傅里叶变换

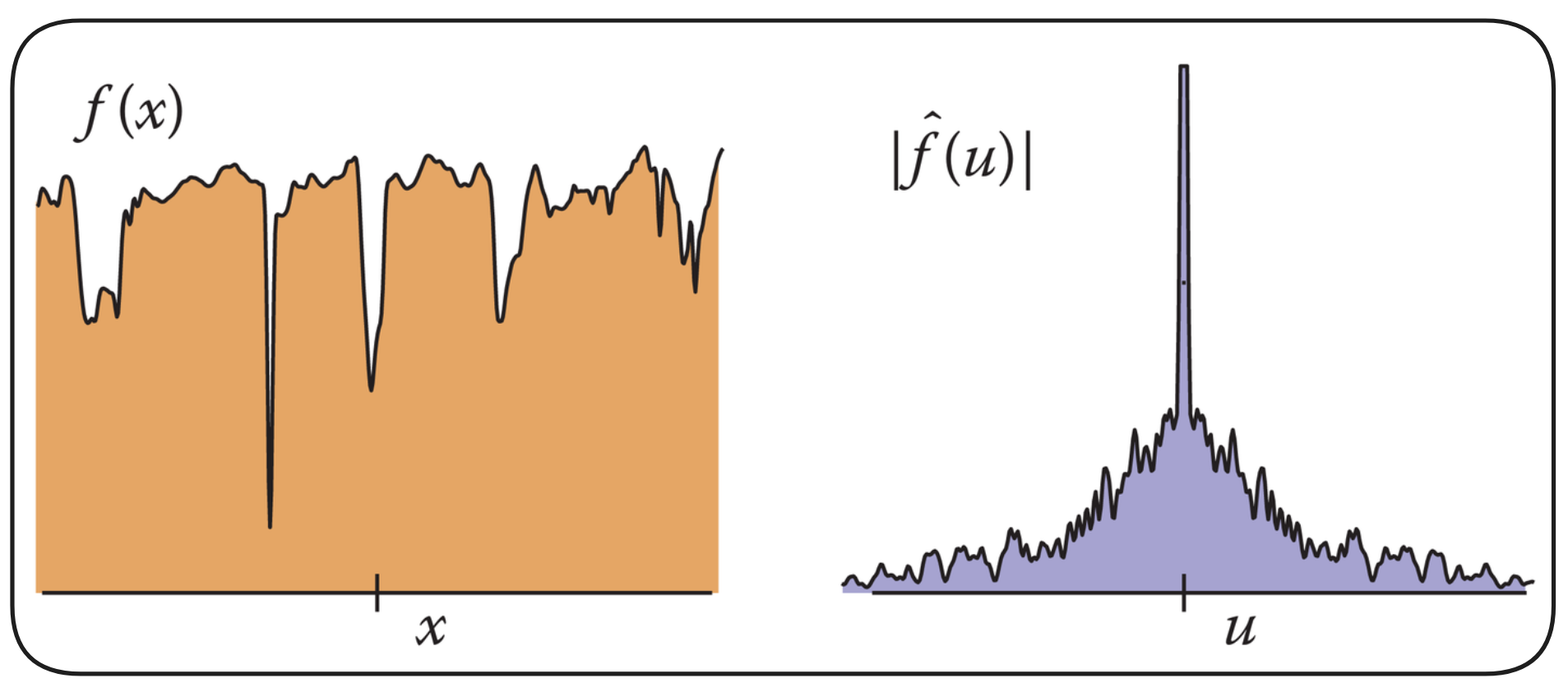
我们之前提到，走样的实质是原图的高频信号被错误采样。图像作为一个 $R^2\rightarrow \text{RGBA
}$的函数，怎么会有高频和低频之分呢？uh actually☝️🤓 我们处理的绝大多数函数都有频域，这个频域可以通过傅里叶变换得到。

先回顾一下傅里叶级数。熟知在 $[-\frac{T}{2},\frac{T}{2}]$ 内，函数 $f(x)$ 可以表示为

$$f(x)=\sum_{n=-\infty}^{\infty}c_n e^{inw_0 x}$$

其中

$$\begin{align*} &c_n=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t)e^{-inw_0t}dt \\ &w_0=\frac{2\pi}{T} \end{align*}$$

这本质上是函数在闭区间内的正交基展开，这个展开的周期为 $T$.

当 $T \rightarrow \infty$ 时，令 $w_n=nw_0$，$\Delta w=w_n-w_{n-1}=w_0$ 再结合积分的定义，我们就能（不太严谨地）求出

$$f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\bigg(\int_{-\infty}^{\infty}f(t)e^{-iwt}dt \bigg)e^{iwx}dw$$

我们可以令 $u=\frac{w}{2\pi}$ 从而去掉积分外面的那个系数

$$f(x)=\int_{-\infty}^{\infty}\bigg(\int_{-\infty}^{\infty}f(t)e^{-2\pi iut}dt \bigg)e^{2\pi iux}du$$

而 $e^{2\pi iux}$ 的系数

$$\hat f(u)=\int_{-\infty}^{\infty}f(t)e^{-2\pi iut}dt$$

就是 $f$ 的傅里叶变换了，它也记作 $\mathcal{F}(f)$.

把 $\hat f$ 代入就得到了逆傅里叶变换

$$f(x)=\int_{-\infty}^{\infty}\hat f(u)e^{2\pi iux}du$$

逆傅里叶变换把函数变成了不同频率的三角函数的积分/求和，这就是我们之前所说的“高频信号”和“低频信号”的含义。之后我们会介绍采样导致高频信号丢失的原因，不过在此之前我们先看看傅里叶变换的一些性质。

傅里叶变换的性质

我们列举傅里叶变换的几个常用的性质。

1. 如果 $f$ 是实函数，$\hat f$ 是偶函数。

2. 函数和傅里叶变换的平方积分相等

   $$\int (f(x))^2dx=\int (\hat f(u))^2du$$

3. 原函数拉长，傅里叶变换收紧

   $$\mathcal{F}(f(x/b))=b\hat f(bu)$$

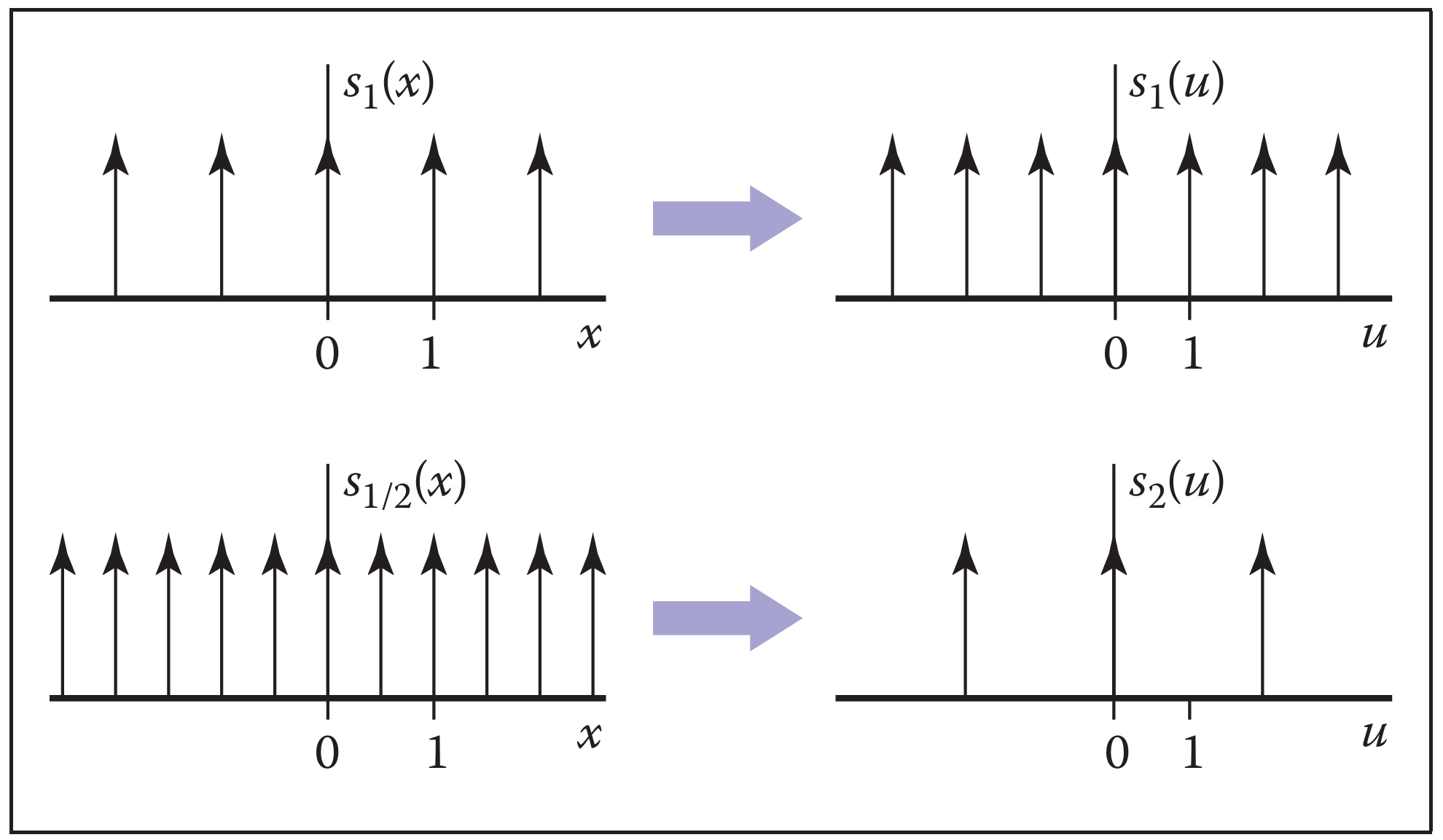
狄拉克脉冲函数和冲激串

狄拉克脉冲函数的定义如下：

$$\delta(t) = \begin{cases} \infty, & t = 0 \\ 0, & t \neq 0 \end{cases}$$

我们可以把连续信号的均匀间隔采样表示为冲激串

$$s_T(x) = \sum_{n=-\infty}^{\infty}\delta(x-nT)$$

与原函数 $f$ 的乘积，这里的 $T$ 表示两个采样点之间的间隔。

$s_T$ 的傅里叶变换为

$$\hat s_T(u)=\frac{1}{T}\sum_{n=-\infty}^{\infty}\delta(u-\frac{n}{T})$$

它仍然是一系列狄拉克函数的和。

卷积定理

之前说过，将 $s_T$ 和原函数 $f$ 相乘能获得许多重要的采样性质，我们很快就会讨论他们了，在此之前我们还要补充最后一个知识——卷积定理。

$$\begin{align*} &\mathcal{F}(f * g) =\hat f\hat g \\ &\mathcal{F}(fg)=\hat f * \hat g \end{align*}$$

这就是说，时域的卷积对应频域的乘积，频域的乘积对应时域的卷积。

走样的原因

一开始我们就说过，走样的实质是原图的高频信号被错误采样。现在我们的数学工具已经足以分析究竟为什么发生了错误采样，以及如何缓解他们了。

先来看看为什么我们没有正确采样高频信号。

假设我们希望对这样的函数进行采样，通过傅里叶变换我们可以得到其频域（右一）

我们之前说过，可以把连续函数的均匀间隔采样表示为冲激串 $s_{T}(x)=\sum_{n=-\infty}^{\infty}\delta(x-nT)$ 和原函数 $f$ 的乘积，而我们也已经知道冲激串的傅里叶变换还是冲激串

$$\hat s_T(u)=\frac{1}{T}\sum_{n=-\infty}^{\infty}\delta(u-\frac{n}{T})$$

再结合卷积定理 $\mathcal{F}(s_Tf)=\hat s_T * \hat f$，以及“卷积就是函数平移后的加权和”，我们就能推出，采样结果的傅里叶变换就是原函数的傅里叶变换的无穷个复制各按 $\frac{n}{T}$ 平移的和。

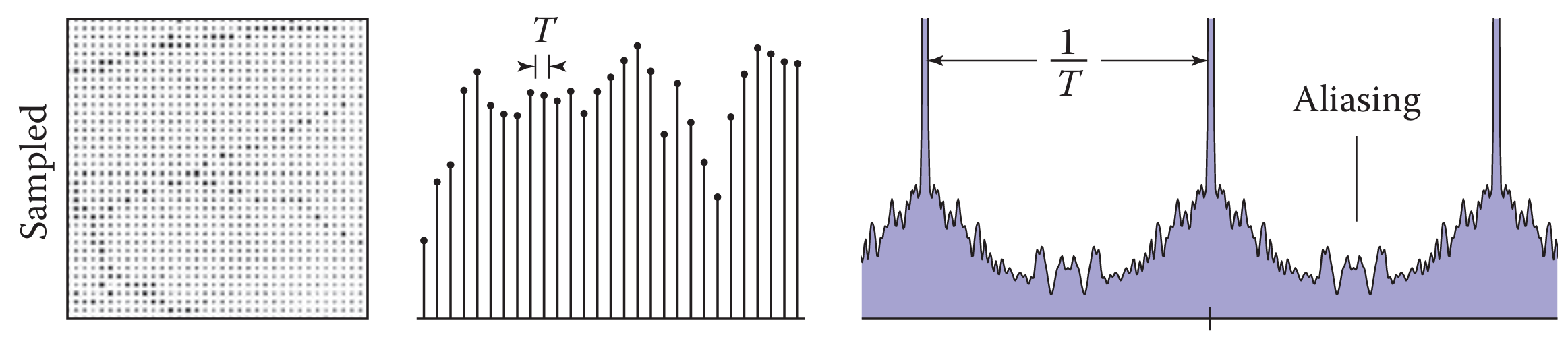
由于我们的采样间隔 $T$ 不够小，即采样率 $\frac{1}{T}$ 不够大，所以相邻的两个复制间发生了重叠，导致高频信号和低频信号产生混合，这就引起了走样。而这正是“高频信号被错误采样”的实质。

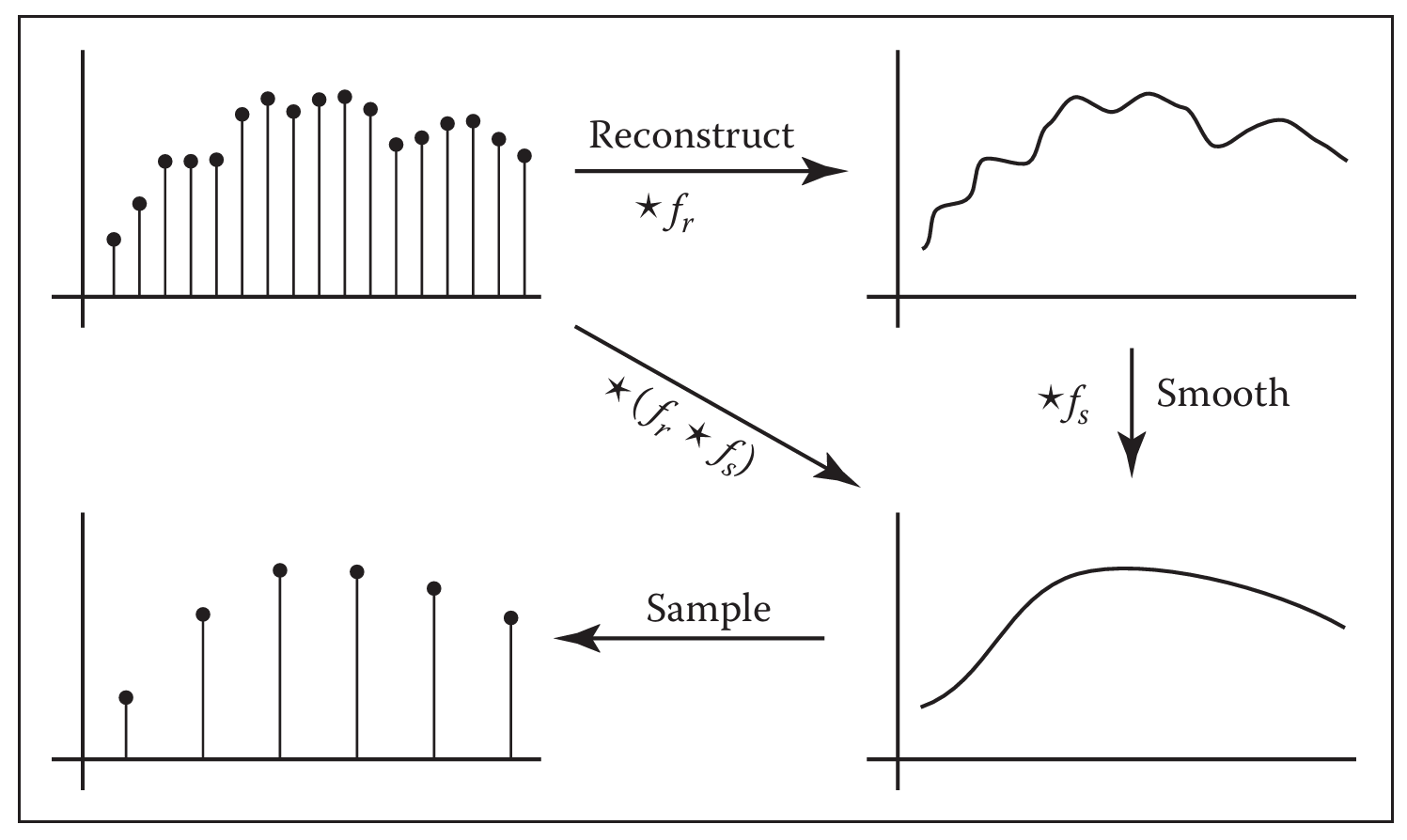
当我们在光栅化时，我们还把像素填上了颜色，这是在“reconstruction”即重建图像。不过由于在采样时我们已经发生了走样，无论怎么重建都不会有一个非常完美的结果了。

滤波器和走样的缓解方法

为了缓解走样，我们自然就要避免发生重叠。避免发生重叠的思路主要有两种：

1. 增加采样率，这样就能让相邻的两个复制距离增大。
2. 用滤波器减弱高频信号的强度。

对图像的光栅化来说，增加分辨率就对应前者；在采样前对原图应用各种滤波器就对应后者。

我们当然会问，增加采样率能缓解走样，那增加到多大合适呢？我们希望相邻的两个复制间的距离足够大以至于不发生重叠，这就需要输入信号的最高频率小于采样频率的一半。采样频率的一半也被称为奈奎斯特频率。理论上说，只要奈奎斯特频率高于被采样信号的最高频率，我们就能完美复原原信号。

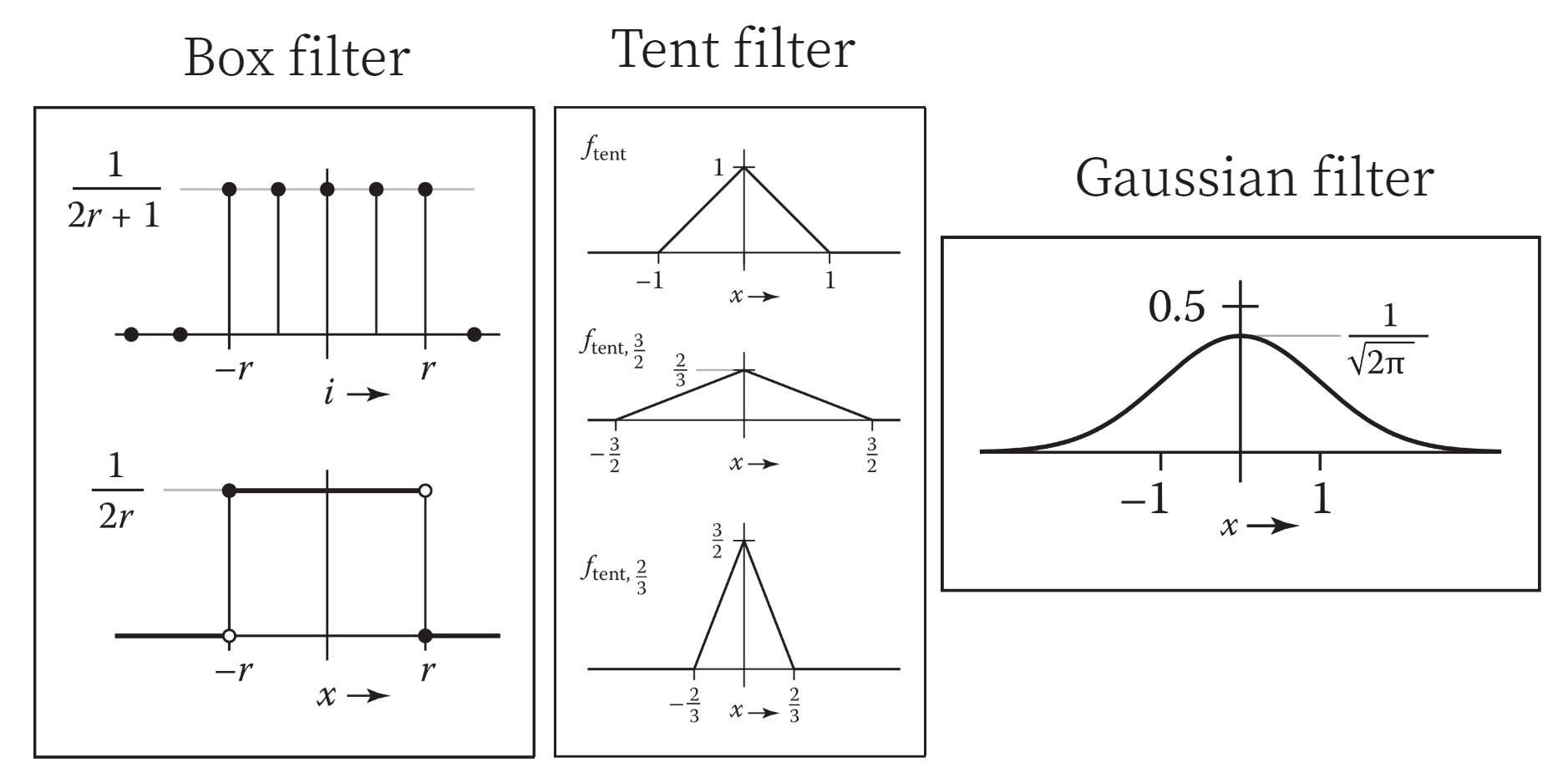
接下来我们看看几个常见的滤波器，它们常被用于和别的函数做卷积。由于我们知道卷积可以被理解为一种“加权平均”，所以我们希望滤波器都是归一化的。

名称	公式
Box filter（离散）	$a_{\text{box},r}[i] = \begin{cases} 1/(2r + 1) & |i| \le r, \\ 0 & \text{otherwise}. \end{cases}$
Box filter（连续）	$f_{\text{box},r}(x) = \begin{cases} 1/(2r) & -r \le x < r, \\ 0 & \text{otherwise}. \end{cases}$
Tent filter	$f_{\text{tent}}(x) = \begin{cases} 1 - |x| & |x| < 1, \\ 0 & \text{otherwise}; \end{cases}$
Gaussian filter	$f_{g, \sigma}(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-x^2/2\sigma^2}$

名称	公式
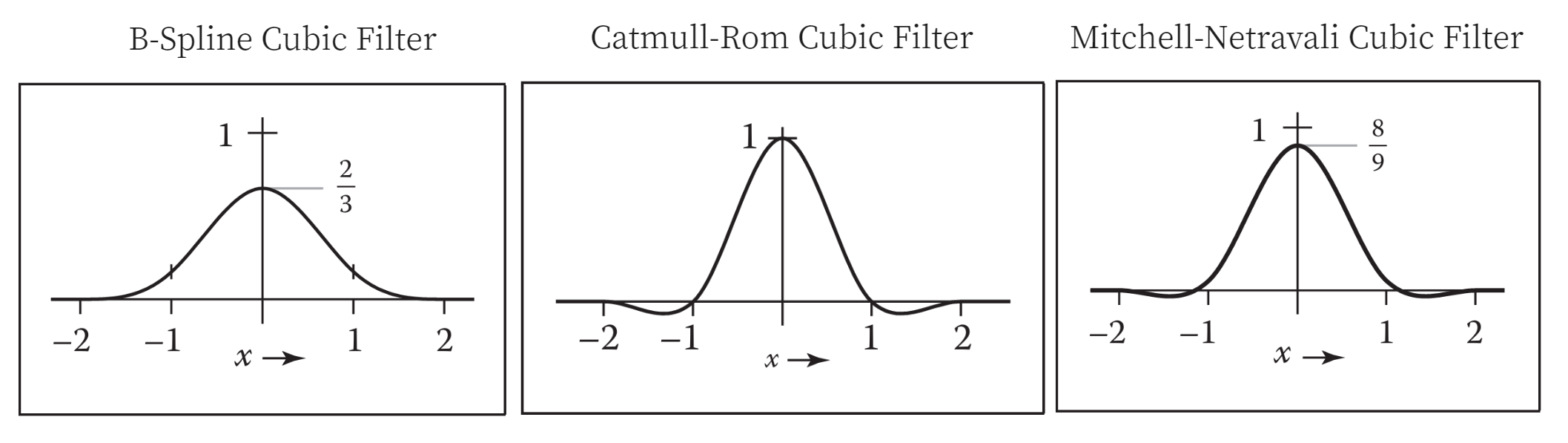
B-Spline Cubic Filter	$f_B(x) = \frac{1}{6} \begin{cases} -3(1 - |x|)^3 + 3(1 - |x|)^2 + 3(1 - |x|) + 1 & -1 \le x \le 1, \\ (2 - |x|)^3 & 1 \le |x| \le 2, \\ 0 & \text{otherwise}. \end{cases}$
Catmull-Rom Cubic Filter	$f_C(x) = \frac{1}{2} \begin{cases} -3(1 - |x|)^3 + 4(1 - |x|)^2 + (1 - |x|) & -1 \le x \le 1, \\ (2 - |x|)^3 - (2 - |x|)^2 & 1 \le |x| \le 2, \\ 0 & \text{otherwise}. \end{cases}$
Mitchell-Netravali Cubic Filter	$f_M(x) = \frac{1}{3}f_B(x) + \frac{2}{3}f_C(x) \\ = \frac{1}{18} \begin{cases} -21(1 - |x|)^3 + 27(1 - |x|)^2 + 9(1 - |x|) + 1 & -1 \le x \le 1, \\ 7(2 - |x|)^3 - 6(2 - |x|)^2 & 1 \le |x| \le 2, \\ 0 & \text{otherwise}. \end{cases}$

除了过滤高频信号之外，滤波器还在重建图像时发挥着重要作用。还记得吗，离散-连续卷积能把一系列离散点变成一个连续函数。在根据采样点重建图像时，我们基本就是在做采样点和滤波器的卷积。在光栅化的“把每个像素点的中心采样颜色填到像素点上”这一步中，我们就是在将采样点和 Box filter 做卷积。

总而言之，为了缓解走样，我们可以以图像细节丰富度为代价，先用低通滤波器滤波，再采样+重建。当然，如果我们有更高分辨率的屏幕就更好了~

其他小知识

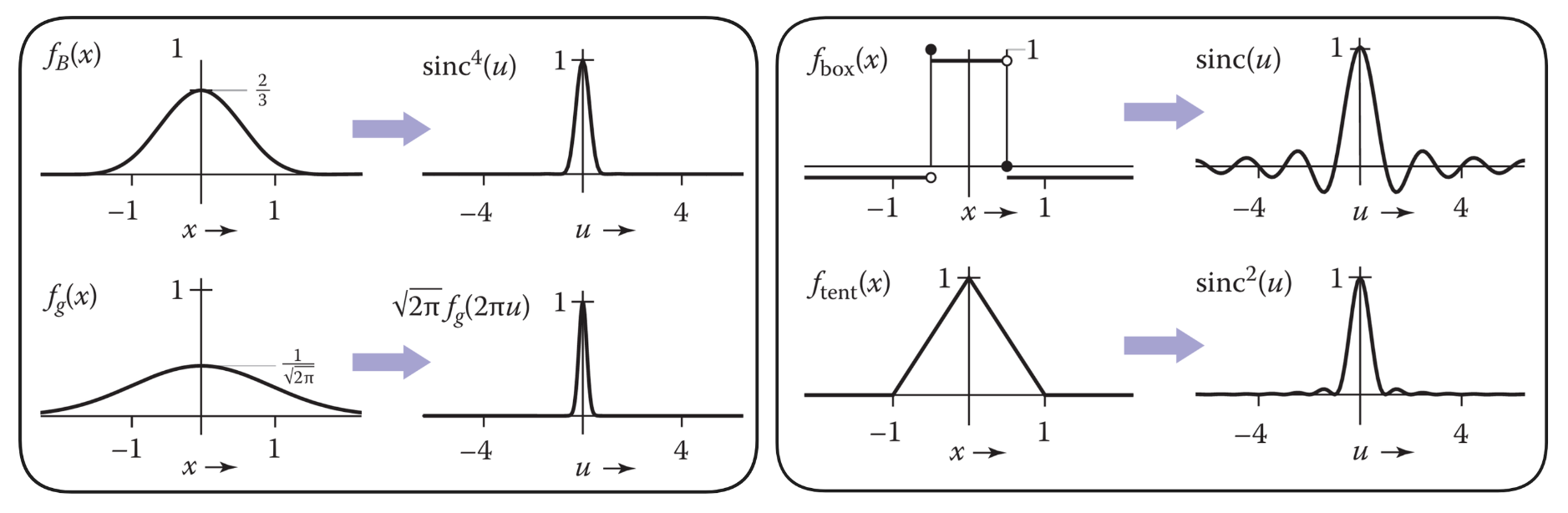
常见滤波器的傅里叶变换

卷积的单位元

任何离散信号和单位脉冲序列做卷积，结果还是原本的离散信号

$$\delta[n] = \begin{cases} 1, & n = 0 \\ 0, & n \neq 0 \end{cases}$$

任何连续信号和狄拉克函数做卷积，结果还是原本的连续信号

$$\delta(t) = \begin{cases} \infty, & t = 0 \\ 0, & t \neq 0 \end{cases}$$

二维卷积和二维滤波器

我们这里只给出连续-连续的二维卷积，别的情况都差不多。

$$\begin{align*} &(f*g)(x,y)=\int\int f(x-x',y-y')g(x',y')dx'dy' \end{align*}$$

对滤波器 $f(x)$，我们简单地定义 $g(x,y)=f(x)f(y)$ 就得到了这个滤波器对应的二维滤波器。一个比较好的性质是，如果 $f$ 是归一化的，那么 $g$ 也是归一化的。

伽马值

显示器的显示亮度关于输入信号不是线性关系。假设输入信号为 $a\in[0,1]$，则有

$$\text{Displayed intensity}=(\text{Maximum intensity})a^\gamma$$

这里的 $\gamma$ 一般在 $2.2$ 左右。虽然在最开始这是 CRT 显示器的物理特性所致，但有趣的是，人眼也恰好对暗部变化比亮部变化更敏感，所以它现在作为一个刻意的设计保留了下来。

伽马矫正在影像系统中也有极大作用。假设我们在拍摄一个苹果的照片，苹果的物理亮度是 $0.5$，相机忠实地把它记录了下来。而当显示器显示时，就显示出了 $0.5^{2.2}\approx
0.22$ 的物理亮度，这显然不是我们想要的。因此在我们拍摄照片之后，相机的图像处理器就会自动对照片进行伽马矫正。

图像锐化

Unsharp Mask 是一个经典的图像锐化算法。令高斯模糊核为 $G$，冲激函数为 $\delta$，它先提取原始图像的高频信号

$$I_{detail} = I_{orig} - I_{orig} * G$$

再把这些高频信号加入回原图中

$$I_{sharp} = I_{orig} + \alpha I_{detail}$$

综合起来就是

$$I_{sharp} =I_{orig}*((1+\alpha)\delta-G)$$

图像缩放

直接对一个像素化的图像采样虽然效率很高，但效果不佳。先用连续的滤波器重建信号，再用低通滤波器过滤高频信号，再采样会得到更好的结果，这被称为 resampling，重采样。