2025-09-13

Assignment 3 Pipeline and Shading

本次作业对 bump_fragment_shader、displacement_fragment_shader 的要求非常不严谨，至少包括这些问题：

这两个 shdaer 需要的贴图是凹凸贴图，凹凸贴图本应该是灰度图，这里使用 RGB 贴图。
在计算切线空间到世界空间的变换矩阵 TBN 时使用了错误的公式。正确的公式需要知道三角形的三个顶点及其 UV 坐标。
displacement 方法没有在光栅化前偏移顶点位置，而只调整了显示颜色。

我们先介绍一下 TBN 的正确计算方式和从 bump texture 算出梯度的方法，再依次介绍一下各个作业的做法。

TBN的正确计算方式

我们先来看看什么是 TBN 以及为什么需要 TBN. 为了简单起见，我们先考虑法线贴图。下文把世界空间里按法线贴图修正后的法线称作“修正法线”，把世界空间里修正前的法线称作“几何法线”，这里默认它们都是归一化的。

考虑世界空间的某一点 $Q$，假设它在法线贴图中对应的一点为 $Q’$，我们知道点 $Q’$ 对应的法线被用于计算世界空间点 $Q$ 的修正法线。但等等，直接把 RGB 值复制过去看起来是错误的，因为随着物体转动，点 $Q$ 对应的法线也应当转动。因此，我们需要一个矩阵来实现这种从法线贴图上的法线到世界空间的修正法线的变换。

贴图是二维的，因此我们再额外定义一个垂直纸面向外的轴 $n$，它表示法线的“默认方向”，这就得到了三维的切线空间。如果点 $Q’$ 对应的法线是 $(0,0,1)$，那么世界空间的点 $Q$ 的修正法线就是原本的几何法线。

接下来就要考虑如何找到这个从切线空间到世界空间的旋转矩阵了。为了简单起见，我们先考虑单个三角形的旋转。之后我们会对每个点求出它自己的旋转矩阵。没错，每个点的旋转矩阵不同，这是因为每个点对应的矩阵会把 $(0,0,1)$ 映射到该点的几何法线，而每个点的几何法线一般不同。

如下图所示，我们希望把法线贴图上的 $P_0’P_1’P_2’$ 旋转为世界空间的 $P_0P_1P_2$，设这里的旋转矩阵为 $M$，世界空间的 $P_0P_1P_2$ 的几何法线为 $\mathbf{n}$，则有

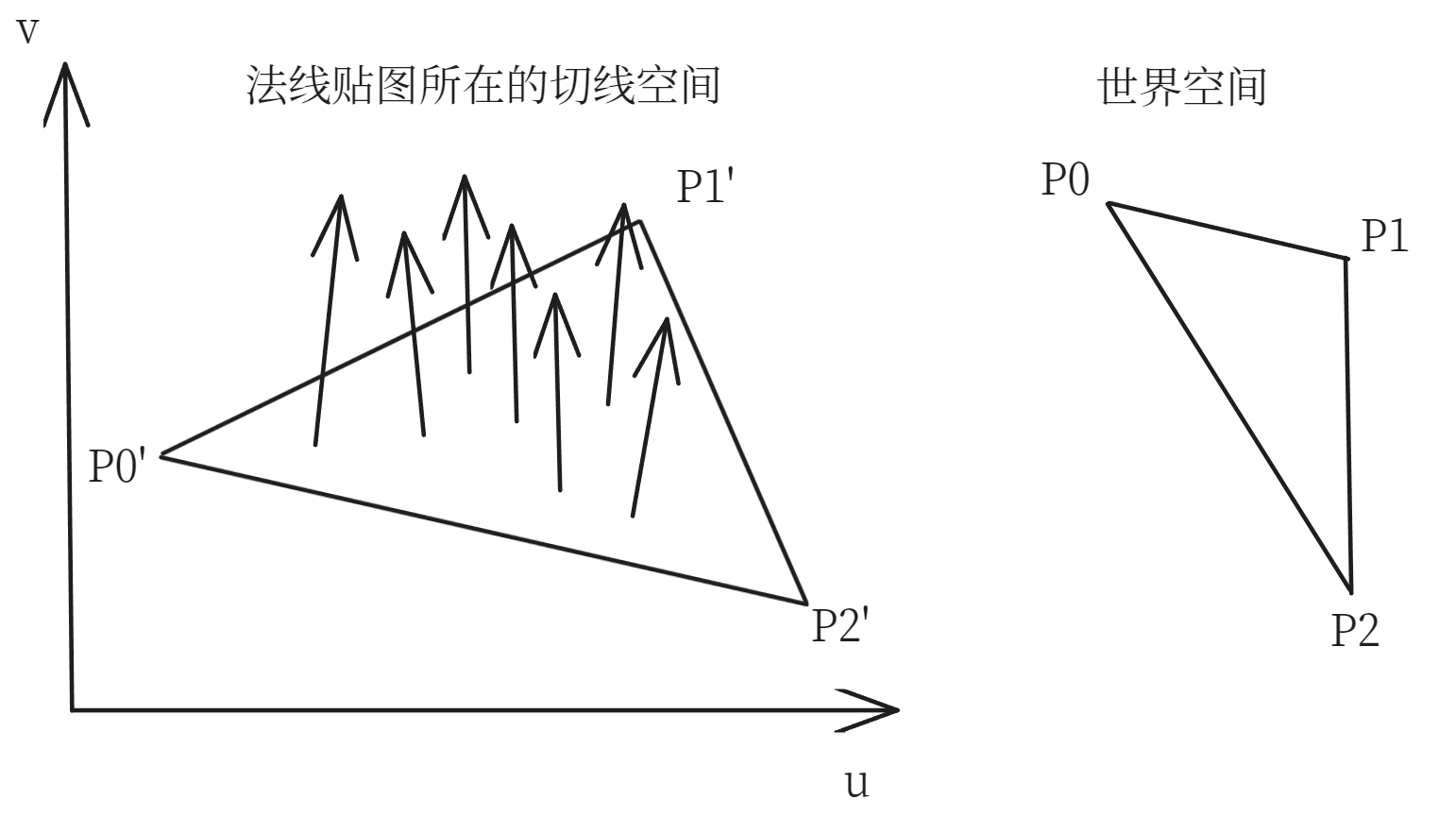
$\begin{align*} &M[0,0,1]^T=\mathbf n \end{align*}$

但光靠这一个方程当然解不出 $M$，所以我们再考虑两个额外的方程：

$\begin{align*} &M (P_1'-P_0')=k(P_1-P_0) \\ &M (P_2'-P_0')=k(P_2-P_0) \end{align*}$

也就是说，我们希望这个矩阵把切线空间三角形的边向量旋转到世界空间的边向量上，这看起来是一个合理的要求。这里的 $k$ 是边的长度的缩放比例，严格来说每条边的缩放比例不一定相等，但只要 UV 映射前后的三角形大体是相似三角形，我们就可以认为缩放比例都为 $k$.

下面我们来解方程。首先我们设

$\begin{align*} &M=\begin{pmatrix} T & B & N \end{pmatrix} \\ &P_1'-P_0'= [\Delta u_1,\Delta v_1,0]^T \\ &P_2'-P_0'= [\Delta u_2,\Delta v_2,0]^T \end{align*}$

下面两个式子利用了 $P_k’$ 的第三个分量为 $0$ 的性质。

结合第一个方程就能得到 $N=\mathbf n$，这里的 $\mathbf n$ 表示世界空间的 $P_0P_1P_2$ 的几何法线。再结合另外两个方程就能得到

$\begin{align*} &\Delta u_1 T+\Delta v_1 B=k(P_1-P_0) \\ &\Delta u_2 T+\Delta v_2 B=k(P_2-P_0) \end{align*}$

之后我们可以解出 $T,B,N$ 的值

$\begin{align*} &T=k\frac{\Delta v_2(P_1-P_0)-\Delta v_1(P_2-P_0)}{\Delta u_1 \Delta v_2-\Delta u_2 \Delta v_1} \\ &B=k\frac{\Delta u_2(P_1-P_0)-\Delta u_1(P_2-P_0)}{\Delta u_2 \Delta v_1-\Delta u_1 \Delta v_2} \\ &N=\mathbf n \end{align*}$

这个公式是不能用的，因为里面有未知数 $k$. 接下来我们解决这个问题。

我们期望 TBN 矩阵是一个旋转矩阵，而旋转矩阵是正交矩阵，所以我们会对 TBN 做施密特正交化和归一化。只要 $P_0P_1P_2$ 和 $P_0’P_1’P_2’$ 大体是相似三角形，那么它们本来就差不多正交（回顾我们对 TBN 的定义，会发现相似说明 TBN 只对 $P_0’P_1’P_2’$ 做了旋转和缩放，这表明 TBN 正交），所以这种正交化不会把 TBN 变化太多。而由于我们会对 TBN 做单位化，所以我们可以放心地令 $k=1$ 来用下面的公式求出 TBN：

$\begin{align*} &T=\frac{\Delta v_2(P_1-P_0)-\Delta v_1(P_2-P_0)}{\Delta u_1 \Delta v_2-\Delta u_2 \Delta v_1} \\ &B=\frac{\Delta u_2(P_1-P_0)-\Delta u_1(P_2-P_0)}{\Delta u_2 \Delta v_1-\Delta u_1 \Delta v_2} \\ &N=\mathbf{n} \end{align*}$

最后，我们希望 N 在正交化前后不变，所以在正交化后我们有

$\begin{align*} &T'=T-(N\cdot T)N \\ &B'=B-(N\cdot B)N-(T'\cdot B)T'/T'^2 \\ &N'=\mathbf n \end{align*}$

再做个单位化就能得到顶点的 TBN 矩阵了。还记得 TBN 矩阵是做什么的吗，我们用它来实现从切线空间到世界空间的变换。所以对点 $Q$，假设其法线贴图对应的法线为 $\mathbf n’$，那么修正后的法线就是 $M_{\text{TBN}}\mathbf n’$.

很好，我们现在能把单个三角形做变换了，但在真正的模型中，每个点的几何法线方向一般都不同，这就意味着它们一般都有不同的 TBN 矩阵。与计算顶点法线类似，我们会找到每个顶点相邻的所有三角形，并对它们的 $T$ 和 $B$ 做加权平均来得到这个顶点的 $T$ 和 $B$.

在实践中，我们一般只计算出每个顶点的 $T$，然后在需要 $B$ 时通过叉乘 $N\times T$ 来计算。对那些非顶点的点，我们用重心坐标插值来算出其 $N$ 和 $T$，然后也做正交化和单位化来保证 TBN 矩阵的正交性。

最后我们再简单分析一下怎么根据凹凸贴图做法线修正。在修正法线时，凹凸贴图与法线贴图的唯一区别就是没有直接给出法线。回顾一下切线空间的定义，我们就可以给凹凸贴图同样设置沿纸面向外的 $n$ 轴，然后把凹凸贴图想象成一个按灰度值起伏的曲面，这个曲面的法线就和法线贴图提供的法线相对应。

具体来说，点 $(u,v)$ 处的法线可以用 $(h(u)-h(u+1,v),h(v)-h(u,v+1),1)$ 来近似，其中 $h(u,v)$ 表示凹凸贴图在点 $(u,v)$ 处的灰度值，$h(u+1,v)$ 表示 $(u,v)$ 右边一格的灰度值。

有时由于我们把贴图做了归一化，我们会改用 $h(u+1/\text{width},v)$，但记住它表示相邻格子的灰度值就行。

最后把这个法线和 TBN 矩阵相乘即可得到修正法线。

参考 Computing Tangent Space Basis Vectors for an Arbitrary Mesh - Eric Lengyel

作业代码

rasterize_triangle

注意这里的插值算法要对所有的属性都做透视矫正，我们简单推导一下透视矫正的公式：

假设我们在对点 $Q$ 的某个属性进行插值，在世界空间中，它所在的三角形为 $P_0P_1P_2$. 投影变换后，它们分别变成了 $Q’$ 和 $P_0’P_1’P_2’$. 用重心坐标分别表示 $Q$ 和 $Q’$，会得到

$\begin{align*} &Q=\alpha P_0+\beta P_1+\gamma P_2 \\ &Q'=\alpha' P_0'+\beta' P_1'+\gamma' P_2' \end{align*}$

这里的 $Q,Q’,P_k,P_k’$ 都是形如 $[x,y,z,1]^T$ 的向量。

在插值属性时，我们希望用 $\alpha, \beta,\gamma$ 来插值，而不是使用 $\alpha’, \beta’,\gamma’$ 插值，因为我们当然不希望属性会因透视位置不同而不同。这就需要我们根据 $\alpha’, \beta’,\gamma’$ 算出 $\alpha, \beta,\gamma$.

不妨设投影变换矩阵为 $M$，则有

$\begin{align*} &MQ=\alpha MP_0+\beta MP_1+\gamma MP_2 \end{align*}$

这里的 $MP_k$ 是形如 $[x_k,y_k,z_k,w_k]^T$ 的用齐次坐标表示的向量，它与形如 $[x,y,z,1]^T$ 的 $P_k’$ 虽然在数学上表示同一个点，但在数值上不同。（还记得吗，齐次坐标下的 $[x,y,z,1
]$ 和 $[ax,ay,az,a]$ 表示同一个点）

因此我们希望对向量的系数做一些调整，来让各个向量变成 $[x,y,z,1]^T$ 的形式，从而找出 $\alpha’, \beta’,\gamma’$ 和 $\alpha, \beta,\gamma$ 的关系。

简单变换一下，我们能把上面的式子写成

$\begin{align*} &MQ=\alpha w_0\frac{MP_0}{w_0}+\beta w_1\frac{MP_1}{w_1}+\gamma w_2\frac{MP_2}{w_2} \end{align*}$

现在右边的各个向量 $\frac{MP_k}{w_k}$ 都已经是 $[x,y,z,1]^T$ 的形式了，我们给它们的系数做个归一化就能让左边的向量也变成 $[x,y,z,1]^T$ 的形式：

$\frac{MQ}{\alpha w_0 + \beta w_1 + \gamma w_2} = \frac{1}{\alpha w_0 + \beta w_1 + \gamma w_2} \bigg( \alpha w_0\frac{MP_0}{w_0}+\beta w_1\frac{MP_1}{w_1}+\gamma w_2\frac{MP_2}{w_2} \bigg)$

由此我们就有

$\begin{align*} &\frac{\alpha w_0}{\alpha w_0 + \beta w_1 + \gamma w_2}=\alpha' \\ &\frac{\beta w_1}{\alpha w_0 + \beta w_1 + \gamma w_2}=\beta' \\ &\frac{\gamma w_2}{\alpha w_0 + \beta w_1 + \gamma w_2}=\gamma' \end{align*}$

解上面的方程的小技巧是借助除法和重心坐标和为 $1$ 的性质得到下面的等价的方程组

$\begin{align*} &\frac{\alpha'}{\beta'}=\frac{\alpha w_0}{\beta w_1} \\ &\frac{\alpha'}{\gamma'}=\frac{\alpha w_0}{\gamma w_2} \\ &\alpha + \beta + \gamma = 1 \end{align*}$

然后就能求出

$\begin{align*} &\alpha = \frac{\alpha' / w_0}{\alpha' / w_0 + \beta' / w_1 + \gamma' / w_2} \\ &\beta= \frac{\beta' / w_1}{\alpha' / w_0 + \beta' / w_1 + \gamma' / w_2} \\ &\gamma= \frac{\gamma' / w_2}{\alpha' / w_0 + \beta' / w_1 + \gamma' / w_2} \end{align*}$

由此，我们就从屏幕空间的重心坐标 $\alpha’,\beta’,\gamma’$ 算出了世界空间的重心坐标 $\alpha,\beta,\gamma$，之后就能用世界空间的重心坐标来正确插值了。

//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array<Eigen::Vector3f, 3>& view_pos) 
{
    auto v = t.toVector4();

    // Find bounding box
    float left = v[0].x();
    float right = v[0].x();
    float bottom = v[0].y();
    float top = v[0].y();
    for (auto& vec: v) {
        left = std::min(left, vec.x());
        right = std::max(right, vec.x());
        bottom = std::min(bottom, vec.y());
        top = std::max(top, vec.y());
    }

    // Update pixels in bounding box
    for (int x = static_cast<int>(left); x <= static_cast<int>(right) + 1; x++) {
        for (int y = static_cast<int>(bottom); y <= static_cast<int>(top) + 1; y++) {
            auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
            // If (x, y) is not inside triangle, continue
            if (alpha < 0 || beta < 0 || gamma < 0) {
                continue;
            }

            // Interpolate z value, color, normal, texcoords, shadingcoords, viewpos
            float alpha_corrected = alpha / v[0].w();
            float beta_corrected = beta / v[1].w();
            float gamma_corrected = gamma / v[2].w();
            float w_reciprocal = alpha_corrected + beta_corrected + gamma_corrected;

            auto z_interpolated = interpolate(alpha_corrected, beta_corrected, gamma_corrected, v[0].z(), v[1].z(), v[2].z(), w_reciprocal);
            auto color_interpolated = interpolate(alpha_corrected, beta_corrected, gamma_corrected, t.color[0], t.color[1], t.color[2], w_reciprocal);
            auto normal_interpolated = interpolate(alpha_corrected, beta_corrected, gamma_corrected, t.normal[0], t.normal[1], t.normal[2], w_reciprocal);
            auto texcoordes_interpolated = interpolate(alpha_corrected, beta_corrected, gamma_corrected, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], w_reciprocal);
            auto viewpos_interpolated = interpolate(alpha_corrected, beta_corrected, gamma_corrected, view_pos[0], view_pos[1], view_pos[2], w_reciprocal);
            
            // A lower z-value means it is displayed in front
            if (z_interpolated < depth_buf[y * width + x]) {
                depth_buf[y * width + x] = z_interpolated;

                fragment_shader_payload payload( color_interpolated, normal_interpolated, texcoordes_interpolated, texture ? &*texture : nullptr );
                payload.view_pos = viewpos_interpolated;
                auto pixel_color = fragment_shader(payload);

                set_pixel(Vector2i(x, y), pixel_color);
            }
        }
    }
}

phong 和 texture

phong 的代码按着 phong 模型实现即可。texture 的代码几乎是一模一样的。

我唯一好奇的地方是为什么末尾乘了 255.0f，难道光照模型的各个数值取值都在 $(0,1)$ 之间？但看光强似乎又不是这样。

Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = payload.color;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = payload.color;
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    Eigen::Vector3f result_color = {0, 0, 0};

    Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
    result_color += ambient;

    for (auto& light : lights)
    {
        // TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular* 
        // components are. Then, accumulate that result on the *result_color* object.

        Eigen::Vector3f vec_to_light = light.position - point;
        Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity / vec_to_light.squaredNorm()) * MAX(0, normal.normalized().dot(vec_to_light.normalized()));

        Eigen::Vector3f vec_to_eye = eye_pos - point;
        Eigen::Vector3f h = vec_to_light.normalized() + vec_to_eye.normalized();
        Eigen::Vector3f specular = ks.cwiseProduct(light.intensity / vec_to_light.squaredNorm()) * pow(MAX(0, normal.normalized().dot(h.normalized())), p);

        // The ambient component is only added once before the for loop
        result_color += (diffuse + specular);
    }

    return result_color * 255.f;
}

Eigen::Vector3f texture_fragment_shader(const fragment_shader_payload& payload)
{
    Eigen::Vector3f texture_color = {0, 0, 0};
    if (payload.texture)
    {
        // TODO: Get the texture value at the texture coordinates of the current fragment
        texture_color = payload.texture->getColor(payload.tex_coords.x(), payload.tex_coords.y());
    }

    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = texture_color / 255.f;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = texture_color;
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    Eigen::Vector3f result_color = {0, 0, 0};
    Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
    result_color += ambient;

    for (auto& light : lights)
    {
        // TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular* 
        // components are. Then, accumulate that result on the *result_color* object.

        Eigen::Vector3f vec_to_light = light.position - point;
        Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity / vec_to_light.squaredNorm()) * MAX(0.0f, normal.normalized().dot(vec_to_light.normalized()));

        Eigen::Vector3f vec_to_eye = eye_pos - point;
        Eigen::Vector3f h = vec_to_light.normalized() + vec_to_eye.normalized();
        Eigen::Vector3f specular = ks.cwiseProduct(light.intensity / vec_to_light.squaredNorm()) * pow(MAX(0.0f, normal.normalized().dot(h.normalized())), p);

        // The ambient component is only added once before the for loop
        result_color += (diffuse + specular);
    }

    return result_color * 255.f;
}

bump 和 displacement

如开头所言，本次作业对这两个 shader 的要求非常不严谨，我们就简单放下代码，不多解释了。在一些不严谨的地方我已经写了注释。

Eigen::Vector3f bump_fragment_shader(const fragment_shader_payload& payload)
{
    
    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = payload.color;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = payload.color; 
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    float kh = 0.2, kn = 0.1;

    // TODO: Implement bump mapping here
    // Let n = normal = (x, y, z)
    // Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
    // Vector b = n cross product t
    // Matrix TBN = [t b n]
    // dU = kh * kn * (h(u+1/w,v)-h(u,v))
    // dV = kh * kn * (h(u,v+1/h)-h(u,v))
    // Vector ln = (-dU, -dV, 1)
    // Normal n = normalize(TBN * ln)

    // Note: The formula is WRONG in theory
    // To calculate the TBN matrix correctly, we need the triangle's vertices and their corresponding UV coordinates
    // read https://learnopengl.com/Advanced-Lighting/Normal-Mapping and 
    // https://terathon.com/blog/tangent-space.html for more details
    float x = normal.x();
    float y = normal.y();
    float z = normal.z();
    float u = payload.tex_coords.x();
    float v = payload.tex_coords.y();
    float w = payload.texture->width;
    float h = payload.texture->height;

    Eigen::Vector3f t = Eigen::Vector3f(x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z));
    Eigen::Vector3f b = normal.cross(t);
    Eigen::Matrix3f TBN;    
    TBN << t, b, normal;

    // In theory the texture should be a grayscale image
    // However we use an ordinary RGB image here, so we take norm
    // read https://games-cn.org/forums/topic/frequently-asked-questionskeep-updating/ for more details
    float dU = kh * kn * (payload.texture->getColor(u+1.0f/w, v).norm() - payload.texture->getColor(u, v).norm());
    float dV = kh * kn * (payload.texture->getColor(u, v+1.0f/h).norm() - payload.texture->getColor(u, v).norm());
    Eigen::Vector3f ln = Eigen::Vector3f(-dU, -dV, 1);

    normal = (TBN * ln).normalized();

    Eigen::Vector3f result_color = {0, 0, 0};
    result_color = normal;

    return result_color * 255.f;
}

Eigen::Vector3f displacement_fragment_shader(const fragment_shader_payload& payload)
{
    
    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = payload.color;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = payload.color; 
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    float kh = 0.2, kn = 0.1;
    
    // TODO: Implement displacement mapping here
    // Let n = normal = (x, y, z)
    // Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
    // Vector b = n cross product t
    // Matrix TBN = [t b n]
    // dU = kh * kn * (h(u+1/w,v)-h(u,v))
    // dV = kh * kn * (h(u,v+1/h)-h(u,v))
    // Vector ln = (-dU, -dV, 1)
    // Position p = p + kn * n * h(u,v)
    // Normal n = normalize(TBN * ln)

    // Note: The formula is WRONG in theory
    // When using Displacement Mapping, the points should be offset in the camera space before rasterizing, 
    // instead of only changing its color
    // read https://learnopengl.com/Advanced-Lighting/Normal-Mapping and 
    // https://terathon.com/blog/tangent-space.html for more details
    float x = normal.x();
    float y = normal.y();
    float z = normal.z();
    float u = payload.tex_coords.x();
    float v = payload.tex_coords.y();
    float w = payload.texture->width;
    float h = payload.texture->height;

    Eigen::Vector3f t = Eigen::Vector3f(x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z));
    Eigen::Vector3f b = normal.cross(t);
    Eigen::Matrix3f TBN;    
    TBN << t, b, normal;

    // In theory the texture should be a grayscale image
    // However we use an ordinary RGB image here, so we take norm
    // read https://games-cn.org/forums/topic/frequently-asked-questionskeep-updating/ for more details
    float dU = kh * kn * (payload.texture->getColor(u+1.0f/w, v).norm() - payload.texture->getColor(u, v).norm());
    float dV = kh * kn * (payload.texture->getColor(u, v+1.0f/h).norm() - payload.texture->getColor(u, v).norm());
    Eigen::Vector3f ln = Eigen::Vector3f(-dU, -dV, 1);

    // In theory we should bias the point using the original normal
    // but to match the homework answer, we bias the point using the corrected normal
    normal = (TBN * ln).normalized();
    point += kn * normal * payload.texture->getColor(u, v).norm();

    Eigen::Vector3f result_color = {0, 0, 0};
    Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
    result_color += ambient;

    for (auto& light : lights)
    {
        // TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular* 
        // components are. Then, accumulate that result on the *result_color* object.
        Eigen::Vector3f vec_to_light = light.position - point;
        Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity / vec_to_light.squaredNorm()) * MAX(0.0f, normal.normalized().dot(vec_to_light.normalized()));

        Eigen::Vector3f vec_to_eye = eye_pos - point;
        Eigen::Vector3f h = vec_to_light.normalized() + vec_to_eye.normalized();
        Eigen::Vector3f specular = ks.cwiseProduct(light.intensity / vec_to_light.squaredNorm()) * pow(MAX(0.0f, normal.normalized().dot(h.normalized())), p);

        // The ambient component is only added once before the for loop
        result_color += (diffuse + specular);
    }

    return result_color * 255.f;
}