存储器层次结构
存储器有多种类型,我们可以根据访问速度把他们排成金字塔结构。靠近上面的访问速度快,靠近下面的访问速度慢。每一层都作为下面一层的缓存(cache),即从下面一层读取数据来加快访问速度:
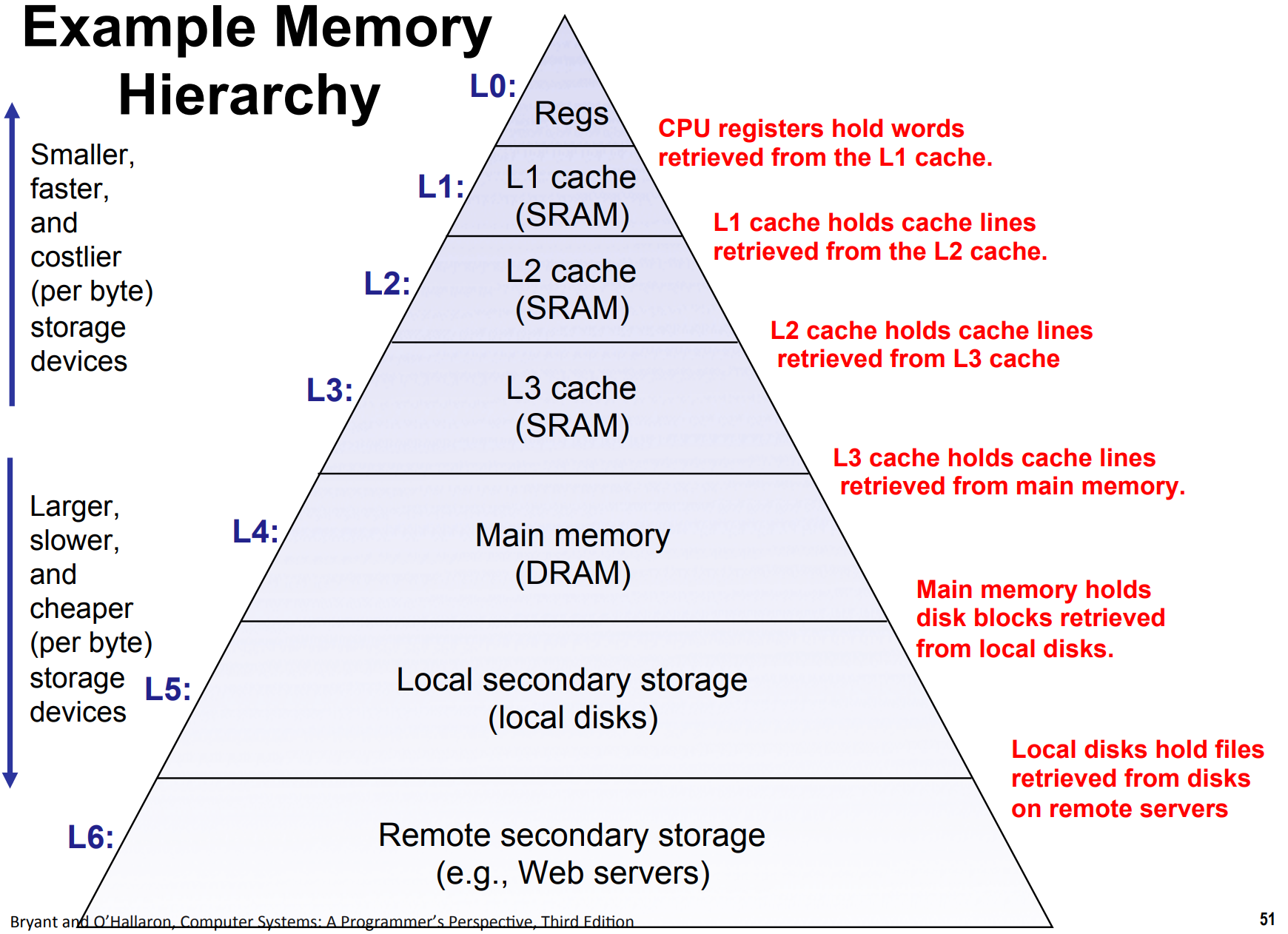
下图比较了不同存储器的访问速度
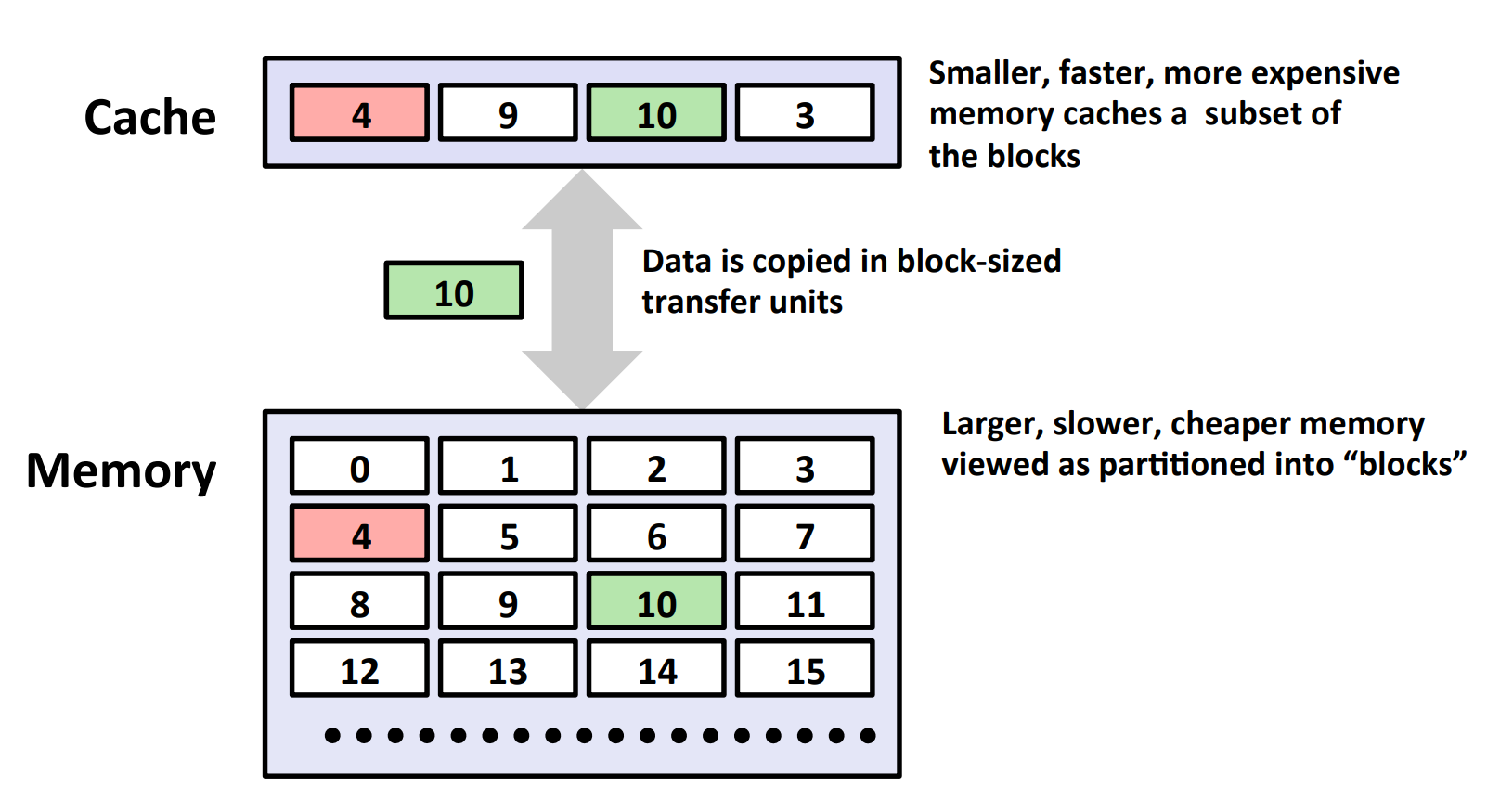
局部性
局部性分为空间局部性和时间局部性。前者指如果一个内存位置被引用,程序可能在将来引用附近的一个内存位置;后者指如果一个内存位置被引用,程序可能在将来再次引用它。
为什么我们希望程序有较好的局部性呢?这是因为访问 cache 比访问 cache 下面一层要快,而 cache 的大小有限,因此我们希望尽可能访问 cache 里的数据。而 cache 存储的数据在空间上和时间上都有一定连续性(参考下面的“高速缓存”一节),所以我们希望程序的局部性好。
如果我们引用了不在 cache 中的数据,这就被称作“缓存不命中”(命中为 “hit”,不命中为“miss”),从而要把 cache 下面一层的数据复制到 cache 中,这是很慢的。
举个例子,一般来说,数组的局部性比链表好,因为链表的地址往往是碎片化的。
高速缓存
高速缓存的结构如图所示:
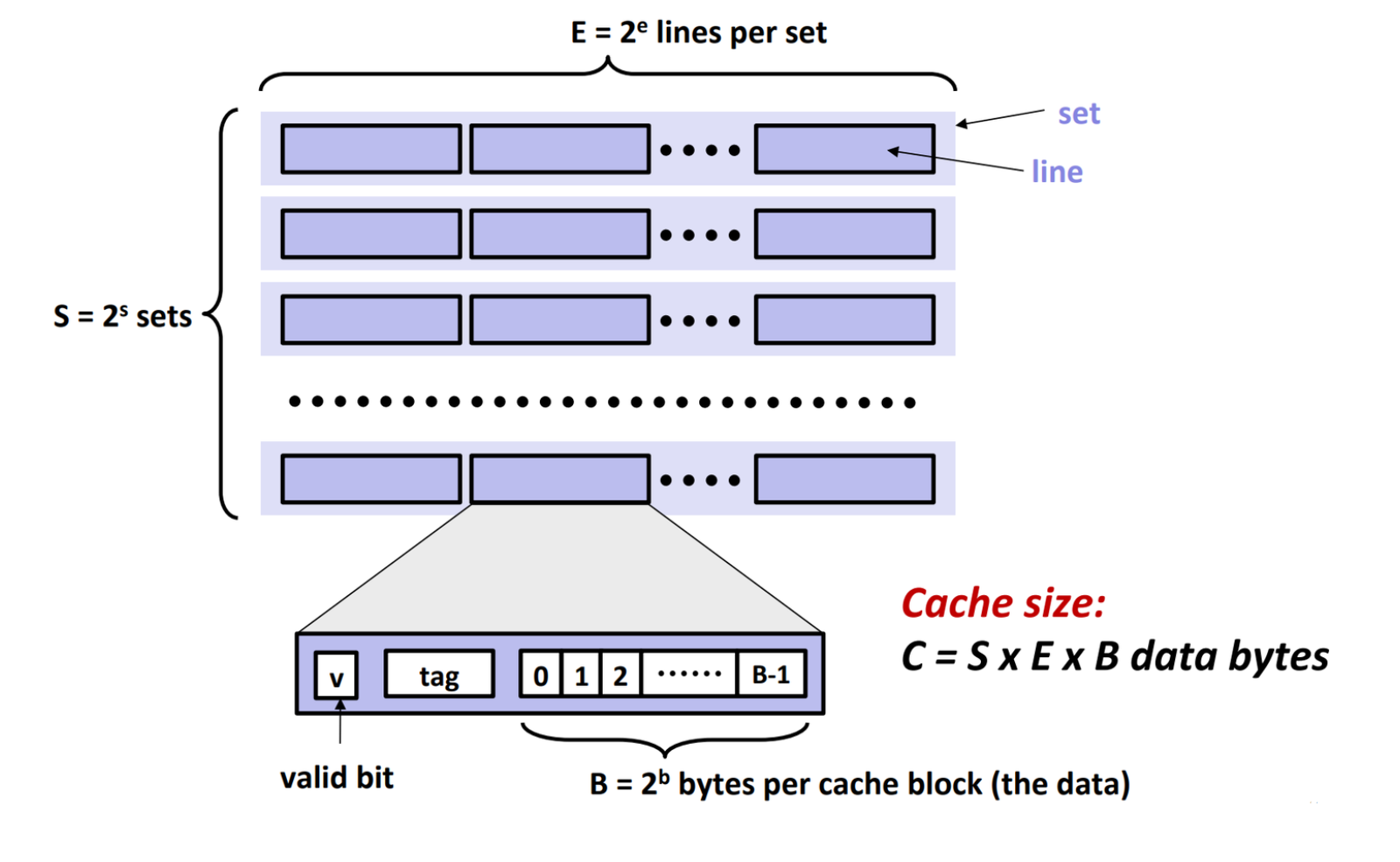
让我们推测一下 line 和 set 是怎么设计出来的。
我们的核心思路是尽量减少高速缓存和主存间交换数据的次数。如果我们能预知未来,我们只要根据未来尽可能把高速缓存填满未来会读的值,然后在需要新值时再读一次就好了。
显然我们不能预知未来,所以我们希望每次的数据交换都尽可能多带来一些“未来可能用到的数据”。所以我们把高速缓存划分成若干个 line,每个 line 都存储一组连续的地址的数据。毕竟如果读到了一个地址,有理由认为它附近的地址在将来会被读到。
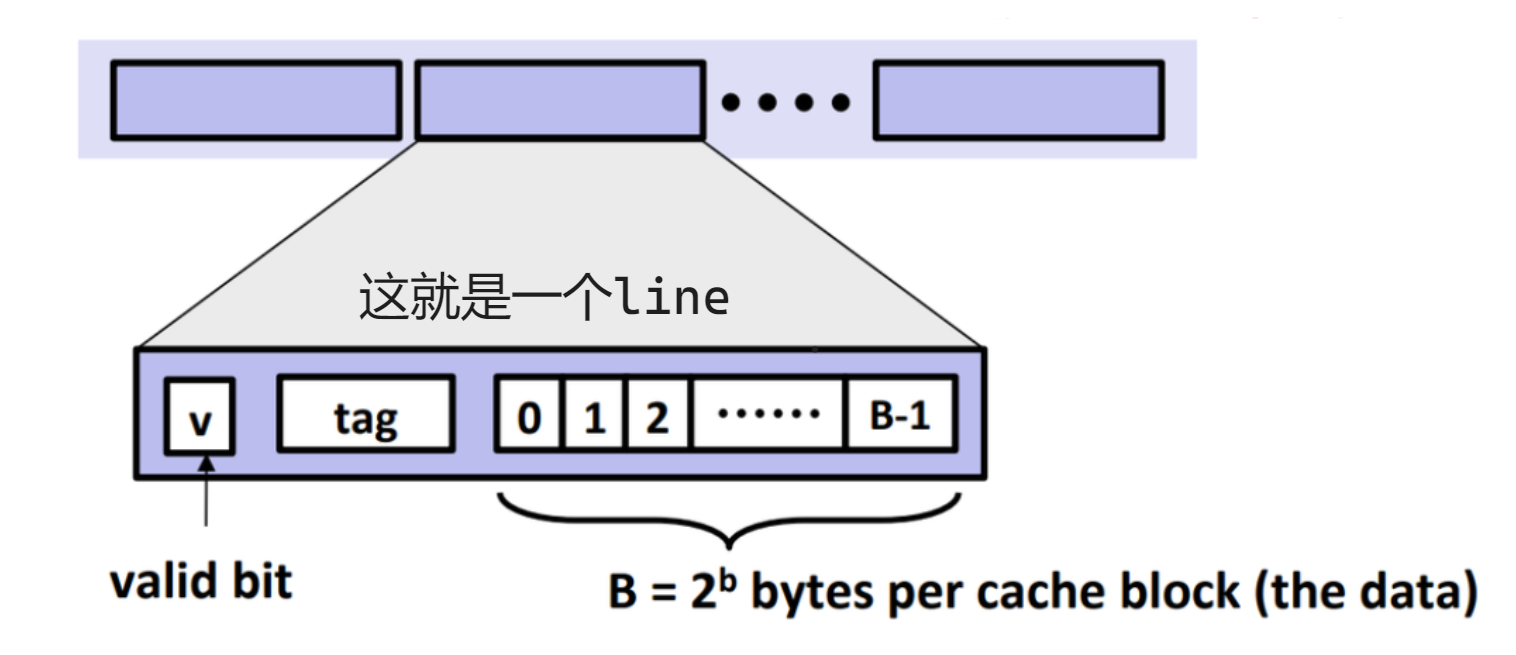
上图给出了 line 的可视化,我们把数据存储在 data 段中,共存储 B 个 bytes.
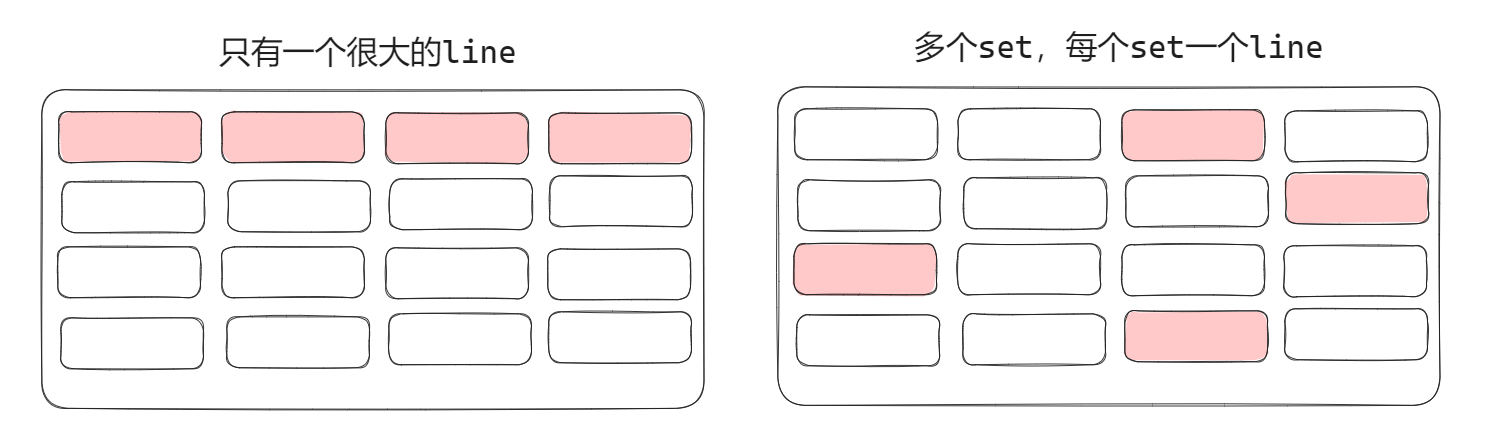
但只是读取连续的一段是不够的。在下图中,我们把主存中需要用到的地址标红。这两种情况中,我们认为右边那种情况更可能在运行时发生,所以我们希望实现多个 set. 如果每个 set 只有一个 line,就实现了直接映射高速缓存。如果每个 set 有多个 line,就实现了组相联高速缓存。
读
接下来我们讲讲如何读取数据,我们以组相联高速缓存为例,毕竟直接映射是组相联的特殊情况。
这里的思路是根据地址找到高速缓冲中对应的 set,然后检查 set 的 line 中是否有当前地址。
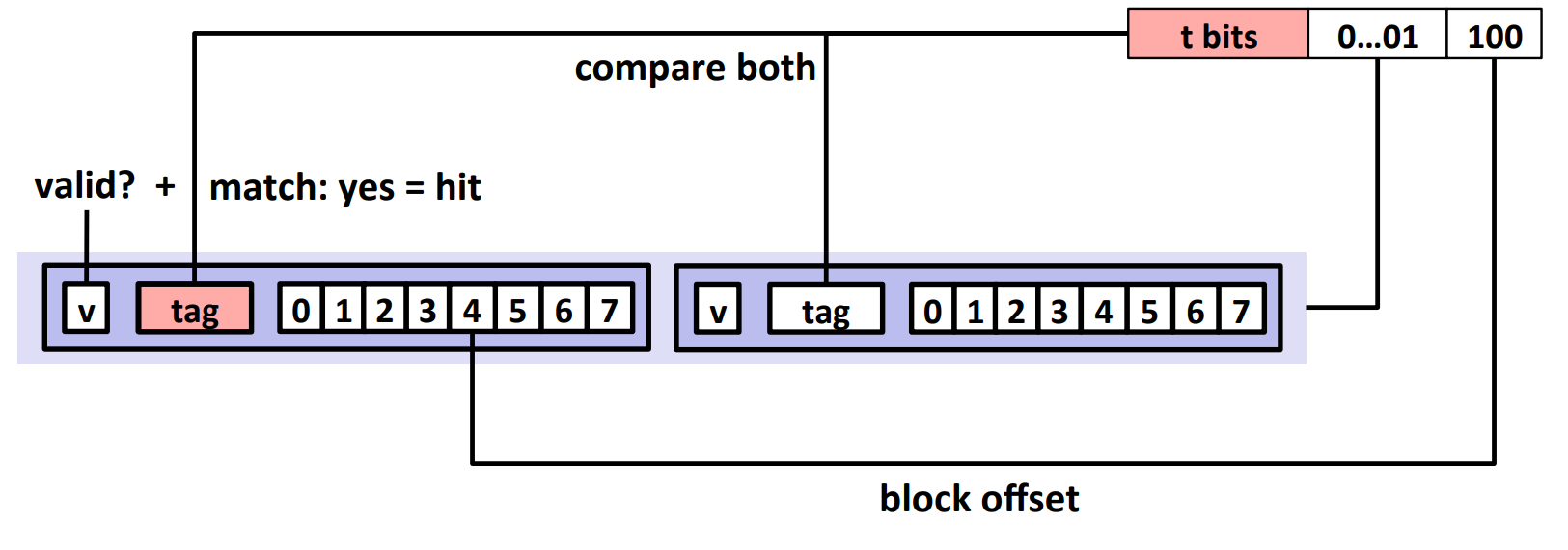
我们把每个地址划分为三个部分,tag 部分、组索引部分、偏移部分。组索引部分在中间,耗费 $\log_2 S$ 个位,用于定位对应的组;tag 部分在最前,占据地址剩下的位置,用于和每个 line 的 tag 作比较从而确定是否有与地址对应的 line;偏移部分在最后,耗费 $\log_2 B$ 个位,用于在找到对应的 line 以后找到对应的数据位置。
所以,对给定的地址,我们先找到它的组索引部分,从而定位对应的组,然后把组里的所有 line 的 tag 和地址的 tag 比较,找到相同的 tag 以后就算是成功命中,然后根据偏移获取对应的值。
如果没找到相同的 tag 呢?这就是不命中了,这时就要让主存和 cache 间交换数据,选一个 line(一般是一组间最久没有被使用的那个)把它替换掉。
写
写比读复杂很多,书上没详细讲,所以我们只是简要提一下。
一个比较靠谱的思路是检查要写的地址是否在 cache 中,如果在就直接写 cache,并标记那个位置为“已修改”。如果不在 cache 中,就像读一样,把那个地址拿到 cache 里来,然后覆写。在 cache 的任何一个地址被覆盖掉时,检查那个地址的值是否已修改,如果修改则覆写主存上的值。
这种做法叫做写回(write-back),尽可能地推迟更新。
要注意的是,由于写是可以推迟的,所以写一般比读要快。
性能例子
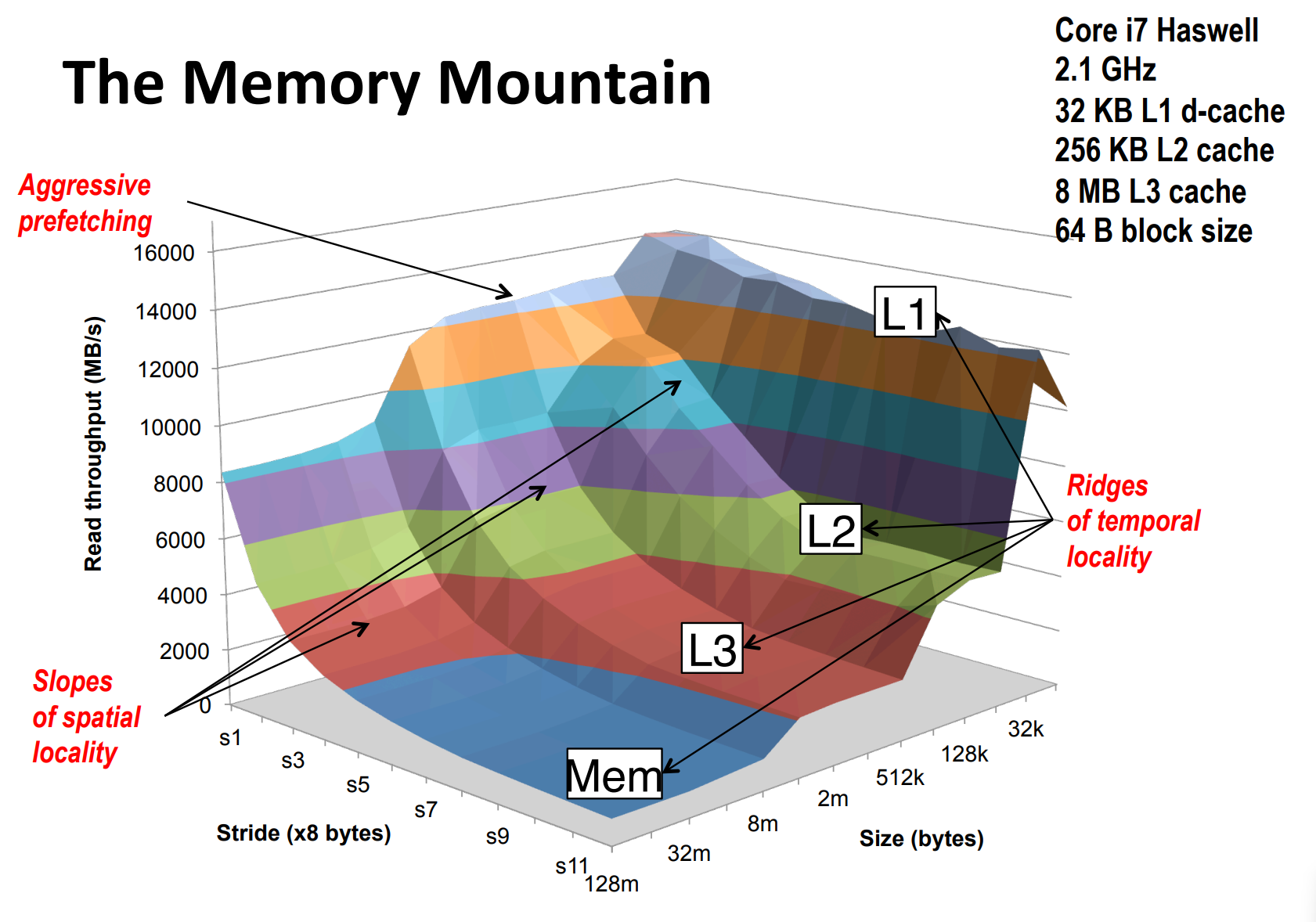
Memory Mountain——数组大小和访问步长影响性能

这张图是对一个大小为 size 的数组以 stride 为步长求和的性能比较。
注意到随着 size 增大,我们愈发往存储器层次结构下面走(比如说,L1 不足以装下所有数据了,我们就不得不走到 L2),同时每走一层时间都有一个猛增。
随着 stride 增大,缓存命中率越来越低,耗时越来越大,直到某个临界点,每次都不命中。
缓存命中影响性能——以矩阵乘法为例
假设我们在做矩阵乘法,我们的高速缓存的每个 line 的 block 能装下 $K$ 个值。
循环顺序对性能的影响
版本 1 是 ijk 循环,a 是行遍历,b 是列遍历,c 不在最内存循环内所以不计性能损耗。对 a 来说,每经过 K 个值,就有一次不命中;对 b 来说,每次都不命中。我们可以认为有这样的缓存不命中率:
| a | b | c |
|---|---|---|
| 1 / K | 1 | 0 |
1 | // 版本1 |
如果把循环顺序改成 ikj,就能得到更好的性能。
这时 a 不在最内层循环,不计性能损耗,b 是行遍历,c 也是行遍历,我们可以认为有这样的缓存不命中率:
| a | b | c |
|---|---|---|
| 0 | 1 / K | 1 / K |
1 | for (i=0; i<n; i++) { |
下图展示了六种循环顺序带来的不同效率:
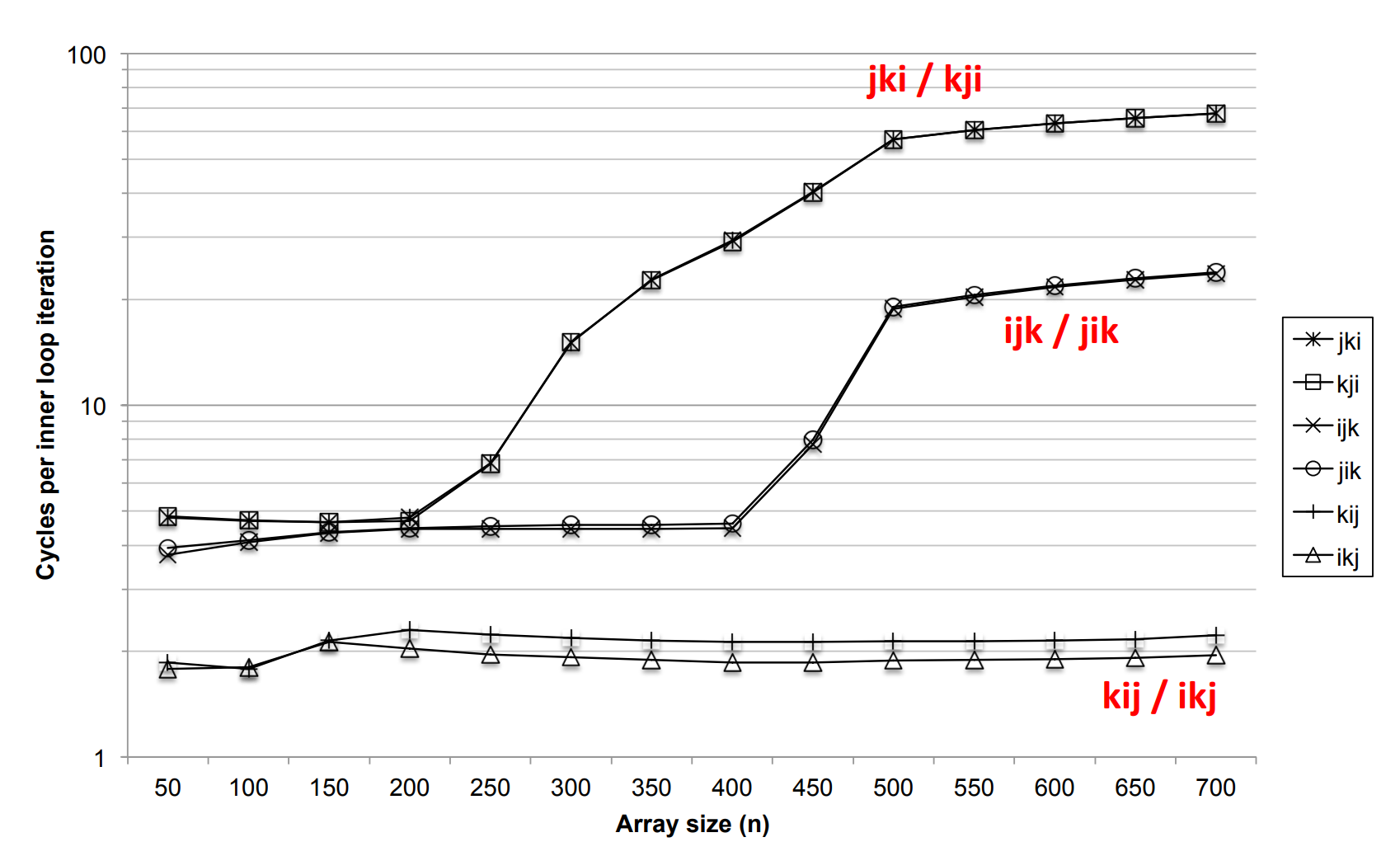
最好的是 ikj 循环,我们可以简单地算出它的大概的总不命中次数。共有 $n^2$ 个值要算,没算一个值大概会不命中 $\frac{n}{K}
- \frac{n}{K}$
次,因此总不命中次数大约为:
$$
n^2 \times (\frac{n}{K} + \frac{n}{K})=\frac{2n^3}{K}
$$
blocking 对性能的影响
其实我们还有更好的优化手段——矩阵分块乘法:
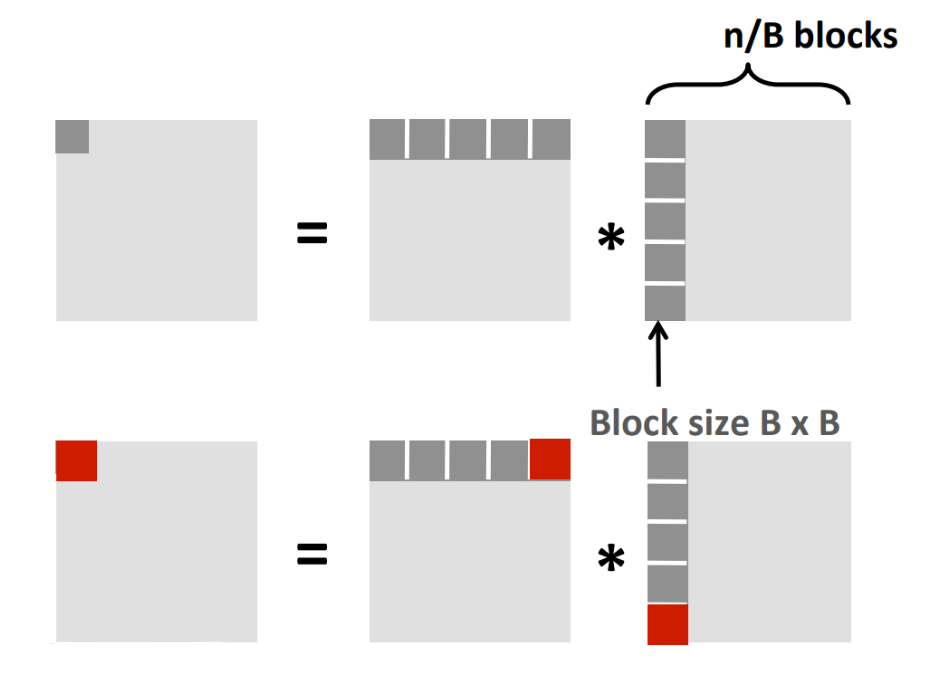
结果里的每个 block 的计算需要访问 $\frac{2n}{B}$ 个小 blck,每个小 block 大概会不命中 $\frac{B^2
}{K}$ 次,因此总不命中次数大约为:
$$
(\frac{n}{B}
)^2 \times \frac{B^2}{K}\times \frac{2n}{B}=\frac{2n^3}{BK}
$$
当然,我们不能无限地增大 $B$. 对于矩阵乘法 C=A×B,我们要同时在缓存中保存 A 的一个块、B 的一个块和 C 的一个块,从而希望有类似 $3B^2 < C$ 的限制(这里的 $C$ 是 cache 的 capacity)。所以尽可能选大的 block,但保证不过大就好。