学习公开课CMU-15-213Notes

第五章——性能优化

文章目录
  1. 1. 编译器的局限性
  2. 2. 用 CPE 表示程序性能
  3. 3. 指令级并行
    1. 3.1. 流水线(Pipeline)
    2. 3.2. 数据流图
  4. 4. 实践

15213 里没讲第四章，我看了下感觉太硬件了于是就跳过了。我们从第五章继续——

一些常见的优化手段我们就不详细说了，简单提一下有这些：

  • 用代码剖析程序找到性能瓶颈
  • 选好的算法
  • 外提循环不变式
  • 减少不必要的内存读写

循环展开技巧性太强，牺牲了可读性，而且说实话性能也没好太多，所以也不详谈。而且大多数编译器在把优化等级设得比较高时会自动做循环展开。

我们主要聊聊——编译器的局限；用 CPE 表示程序性能；指令级并行。

编译器的局限性

编译器对程序只使用安全的优化，因此有些我们脑补编译器会优化的东西实际上不会被优化。

1
2
3
4
5
6
7
void add1(long *x1, long *x2) {
	*x1 += *x2;
	*x1 += *x2;
}
void add2(long *x1, long *x2) {
	*x1 += *x2 * 2;
}

乍一看这两个函数功能相同，且下面那种读写内存次数更少，或许我们会期望编译器把上面的版本优化成下面的版本。

可其实两者功能并不完全相同。考虑两个指针指向同一个对象的情况。

因此，要很仔细才能写出编译器能顺利优化的代码。

用 CPE 表示程序性能

CPE 即 Cycles Per Element，计算方法如下：

CPE = Total Cycles / Number of Elements，即总周期数 / 元素数量。

实际的 CPE 值很难仅通过代码分析准确预测，需要在特定硬件、编译器配置下通过实际测试获得准确值。一般来说，我们通过性能分析工具来得到总周期数，然后根据任务得出其元素数量，从而算出 CPE。

指令级并行

现代处理器并不是顺序执行指令的，顺序执行只是一种抽象。指令执行的顺序不一定要与它们在机器级程序中的顺序一致。这让我们实现了指令级并行。

这里的内容太多太硬核了，我也没理解，就只讲讲指令级并行的大体概念和流水线吧。

大体来说，处理器会分析程序里每条指令的依赖关系，从而并行执行没有依赖关系的指令。

例子：

假设我们有指令序列:

1
2
3
4
5
6
1. mov eax, [mem1]    # 从内存加载数据到eax
2. add ebx, ecx       # 将ebx和ecx相加，结果存入ebx
3. mul eax, 4         # 将eax乘以4
4. add edx, ebx       # 将ebx和edx相加，结果存入edx
5. mov [mem2], eax    # 将eax存入内存

依赖关系图:

1
2
3
4
5
6
7
8
9
10
11
     指令1           指令2
 (mov eax, [mem1])  (add ebx, ecx)
       |                 |
       v                 v
    指令3              指令4
 (mul eax, 4)       (add edx, ebx)
       |
       v
     指令5
(mov [mem2], eax)

这时我们可能就会并行执行指令 1 和指令 2.

流水线(Pipeline)

流水线将单条指令的执行阶段（取指、解码、执行、访存、写回）拆分成多个步骤，每个步骤由不同的硬件单元处理，从而可以同时处理多条处于不同步骤的指令。例如，一个典型的浮点加法器包含三个阶段：一个阶段处理指数值，一个阶段将小数相加，另一个阶段对结果进行舍人。这种技术增加了吞吐量（Throughput），但单个指令的执行延迟并不会减少。

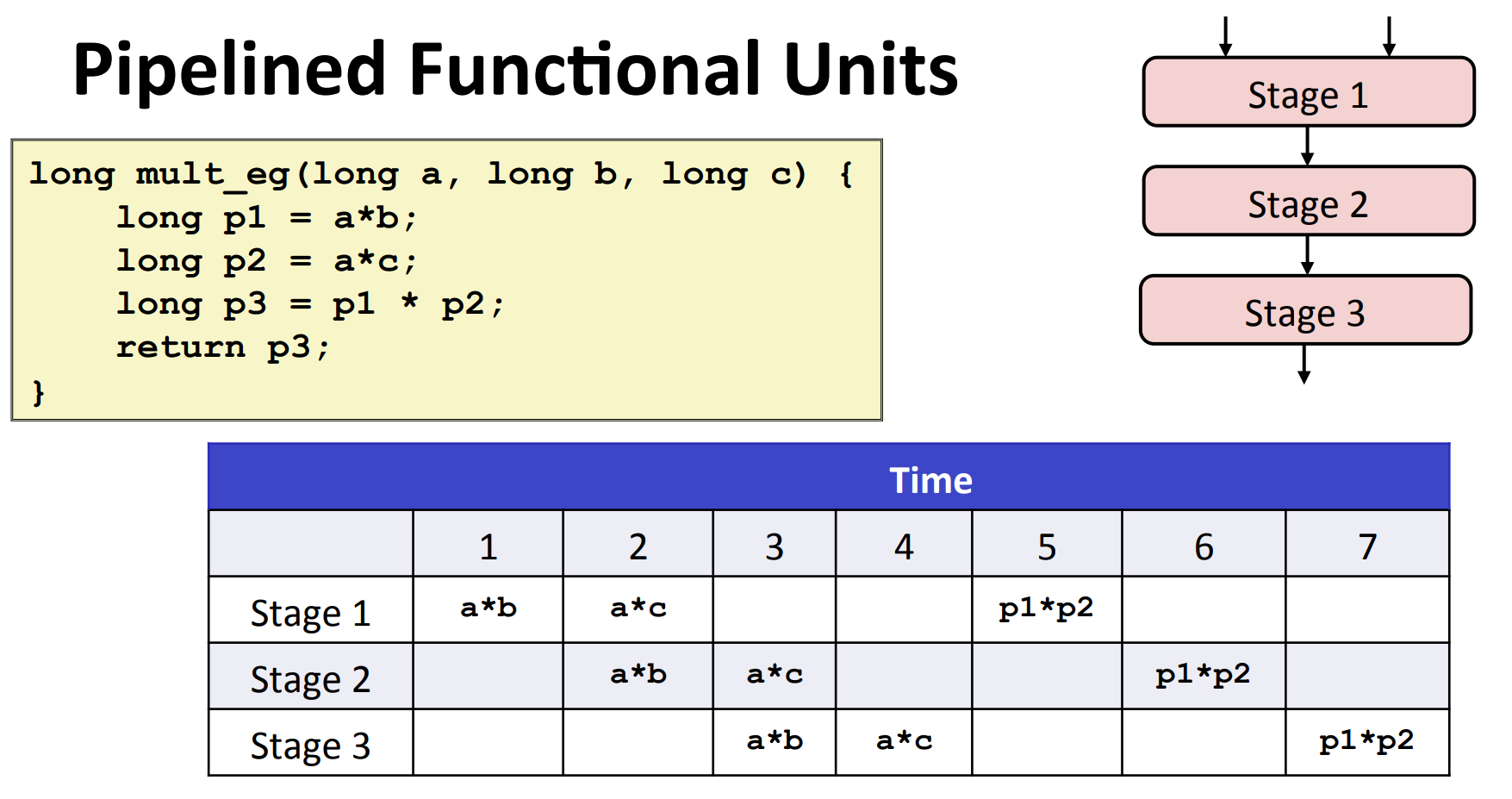
数据流图

我们可以通过程序的数据流图来粗糙地分析程序的指令级并行程度。这里举一个例子应该就足够了。假设我们想算 $\sum_{k=0}^{n}a_kx^k$，下面有两种算法：

在 poly 中，我们共做了 n 次加法，2n 次乘法

1
2
3
4
5
6
7
8
9
10
11
double poly(double a[], double x, long degree)
{
    long i;
    double result = a[0];
    double xpwr = x;  /* Equals x^i at start of loop */
    for (i = 1; i <= degree; i++) {
        result += a[i] * xpwr;
        xpwr = x * xpwr;
    }
    return result;
}

在 polyh 中，我们共做了 n 次加法，n 次乘法

1
2
3
4
5
6
7
8
9
/* Apply Horner's method */
double polyh(double a[], double x, long degree)
{
    long i;
    double result = a[degree];
    for (i = degree-1; i >= 0; i--)
        result = a[i] + x*result;
    return result;
}

然而实际上 poly 速度更快，为什么呢？因为 poly 有更好的指令级并行度。

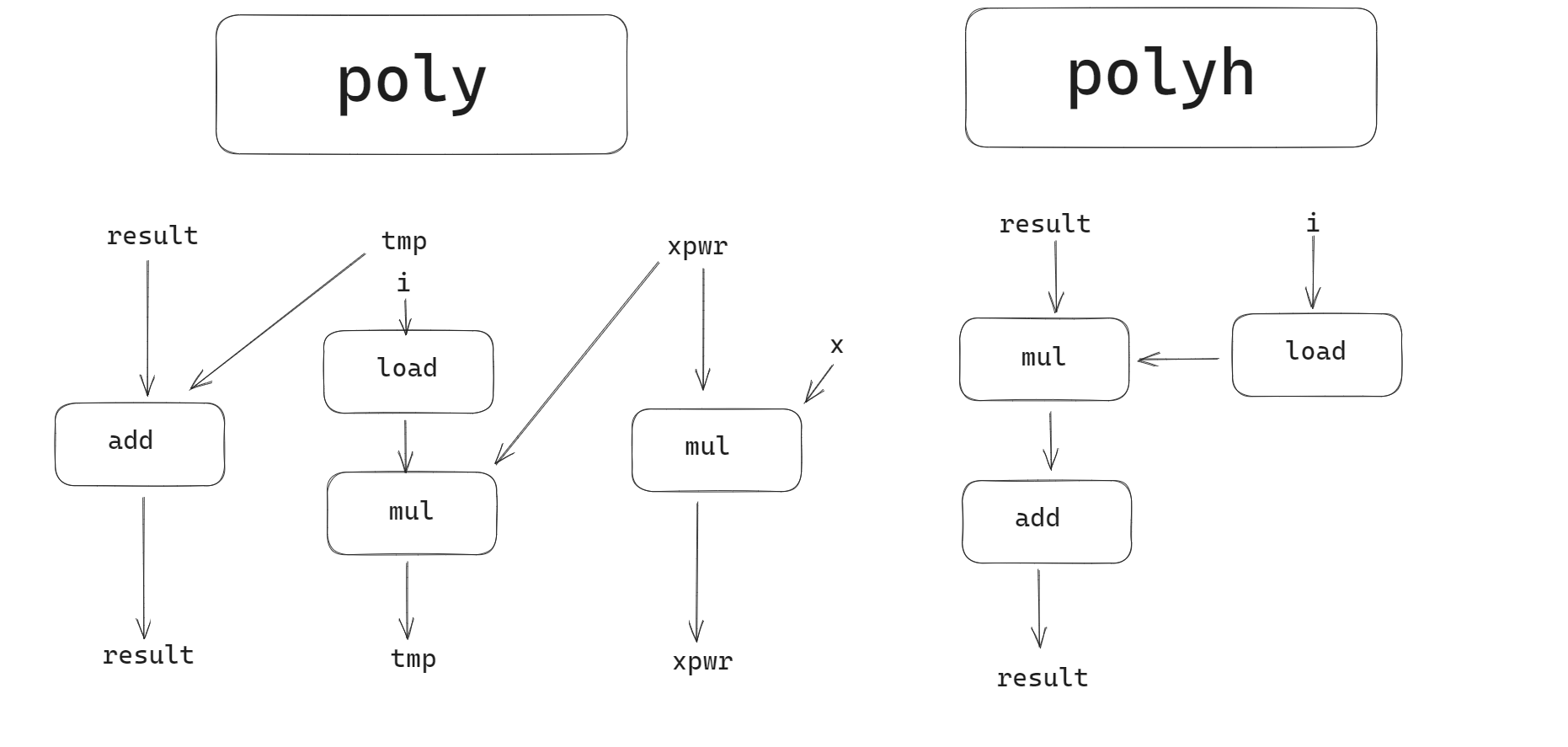
poly 的关键路径是 mul，polyh 的关键路径则是 mul → add.

实践

之前做 leetcode 还遇到了一则趣事（3356. Zero Array TransformationⅡ）

那题的解法里需要构造这样的函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool iskZeroArray(vector<int> &nums, vector<vector<int>> &queries, int k) {
    vector<int> ops(nums.size() + 1, 0);
    for (int i = 0; i < k; i++) {
        int l = queries[i][0];
        int r = queries[i][1];
        int val = queries[i][2];
        ops[l] += val;
        ops[r + 1] -= val;
    }

    int n = nums.size();
    int op = 0;
    for (int i = 0; i < n; i++) {
        op += ops[i];
        if (op < nums[i]) {
            return false;
        }
    }
    return true;
}

在 iskZeroArray 的第一个 for 循环中, 我写的原本是

1
2
3
4
vector<int> query = queries[i];
int l = query[0];
int r = query[1];
int val = query[2];

但是这样的程序耗时 1000 ms. 换成

1
2
3
int l = queries[i][0];
int r = queries[i][1];
int val = queries[i][2];

后，50ms. 两者甚至都是 O(N)的，前者之所以如此慢应该是因为不断分配内存给 query 吧.