第二章——计算机内的信息表示

文章目录

1. 1. 整数
   1. 1.1. 表示
   2. 1.2. 加法，乘法，左右移
   3. 1.3. 不同类型的整数一起运算会发生什么？
   4. 1.4. 注意事项
2. 2. 浮点数
   1. 2.1. 表示
   2. 2.2. 舍入（四舍五入）
   3. 2.3. 加法，乘法
   4. 2.4. 类型转换
3. 3. 杂项
   1. 3.1. 大端法和小端法

我们知道，在 32 位机器上和 64 位机器上，相同的 C 语言数据类型可能占用不同的字节数：

C declaration		Bytes
Signed	Unsigned	32-bit	64-bit
[signed] char	unsigned char	1	1
short	unsigned short	2	2
int	unsigned	4	4
long	unsigned long	4	8
int32_t	uint32_t	4	4
int64_t	uint64_t	8	8
char *		4	8
float		4	4
double		8	8

整数

表示

整数的表示可以分为 unsigned 和 signed，前者只能表示非负数，后者可以表示整数。下面是各个整数类型占用的字节数：

C declaration		Bytes
Signed	Unsigned	32-bit	64-bit
short	unsigned short	2	2
int	unsigned	4	4
long	unsigned long	4	8

众所周知，signed 的表示采用补码表示，就是模 $2^m$ 意义下对应的最小正数的二进制表示，其中 $m$ 是耗费的 bits 数。

下面的例子中类型是 signed short，$15213$ 的表示就是它的二进制表示，而 $-15213$ 的表示实际上是 $-15213 + 2^{16}$ 的二进制表示。

	Decimal	Hex	Binary
x	15213	3B 6D	00111011 01101101
y	-15213	C4 93	11000100 10010011

让我们假设二进制表示为 $b{w-1},b{w-2},…,b_1,b_0$，那么如果是 unsigned，其值为

$$\sum_{k=0}^{w-1}2^{k}b_k$$

如果是 signed，当 $b_{w-1}$ 即最高位不为 1 时，把二进制转换成十进制即可。

当最高位为 1 时，其值为

$$-2^{w}+\sum_{k=0}^{w-1}2^{k}b_k$$

不难注意到能表示的整数有上下限，参考下表：

Signed	Unsigned	64-bit
short [-32768, 32767]	unsigned short [0, 65535]	2
int [-2^31, 2^31-1]	unsigned int [0, 2^32-1]	4
long [-2^63, 2^63-1]	unsigned long [0, 2^64-1]	8

加法，乘法，左右移

加法和乘法就是模意义下的加法和乘法，所以你喜欢的运算规律都符合。“溢出”也只是模了一下。

而左右移呢？左移不难理解，把它的表示统一往左边移动，移出范围了就扔掉，最低位填充 0.

x << m 实际上是在做 $2^{m}x
(\text{mod $2^w$})$.

右移则分为逻辑右移和算术右移，前者是在右移后在最高位上填充 0，后者在最高位上填充符号位。

对 unsigned 来说它们没有区别，毕竟 unsigned 不考虑符号，但对 signed 来说就不一样了。

大多数 C 编译器对有符号整数实现的是算术右移，x >> m 实际上是在做 $\lfloor \frac{x}{2^m} \rfloor$.

不同类型的整数一起运算会发生什么？

核心思想是，在尽量保证值不变的前提下把数进行扩展。

把一个 signed short 整数和 signed int 相加会发生什么呢？我们会进行“符号扩展”，把 signed short 扩展成 signed int 再做加法，返回一个 signed int。

那，什么是符号扩展呢？如果 short 值是正数，高位会用 0 填充；如果是负数，高位会用 1 填充（符号扩展）。uh actually 🤓☝️ 这是在保证值不变的前提下把 short 转换成 int。

把一个 unsigned int 整数和 signed long 相加会发生什么呢？我们会把 unsigned int 扩展为 signed long（即在前面加 0）再做加法，返回一个 signed long。

当然，也有不能保证值不变的情况。比如 unsigned int 和 signed int 相加时，我们会把 signed 转换成 unsigned 再求和。

所以说，拜托不要写这种奇怪的代码：

signed int a = -1;
unsigned int b = 1;

if (a < b) {
    printf("a < b\n");
} else {
    printf("a >= b\n");
}

上面的代码会输出 $a\geq b$，你这是在破坏数学的世界观！

注意事项

unsigned 很可能造成错误。对下面的代码，你觉得哪个是对的？

unsigned i;
for (i = cnt-2; i < cnt; i--)
	a[i] += a[i+1]

unsigned i;
for (i = cnt-2; i >= 0; i--)
	a[i] += a[i+1]

答案是前者，因为对后者来说，i = 0 以后 i-- 会让 i 溢出变为正数，导致无限循环。

反正不要写这样的代码，你这是在破坏数学的世界观！

浮点数

表示

按照 IEEE 标准，浮点数的表示如下：

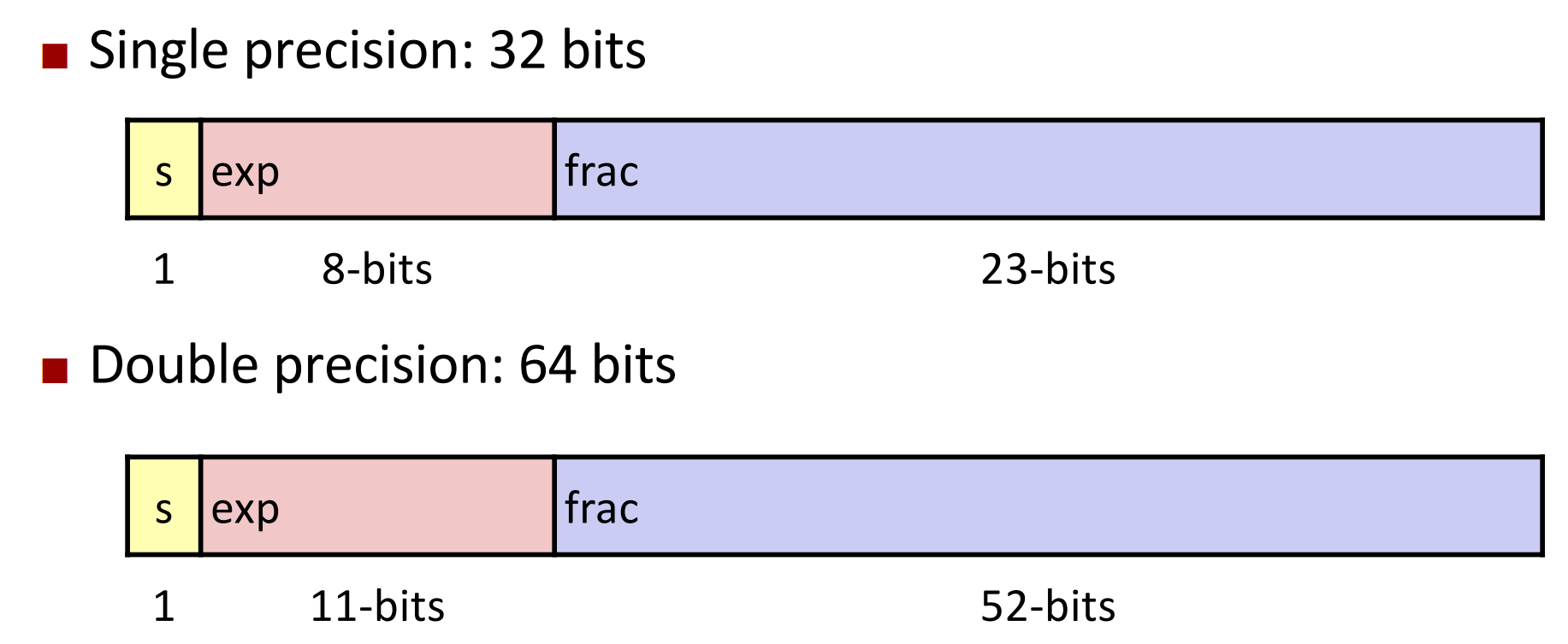
其中 s 是符号位，0 表示正数，1 表示负数

计算方式大致为

$$(-1)^s \times 2^{\text{exp}-\text{bias}}\times(1\text{.frac})$$

之所以说是“大致”，是因为还存在几种特殊情况。

如果 exp 全是 0，我们称其为非规格化数（denormalized），使用下面的公式计算：

$$(-1)^s \times 2^{1-\text{bias}}\times(1\text{.frac})$$

如果 exp 全是 1，frac 全是 0，我们认为表示的是 infin. 至于是 $+\inf$ 还是 $-\inf$ 由符号位决定。

如果 exp 全是 1，frac 不为 0，表示 NaN（not a number）.

看起来确实是很奇怪的标准！这涌现出的结果是，能表示的值在靠近 0 的位置比较密集，在远离 0 的位置比较稀疏。（下图以 exp 占 3 bits，frac 占 2 bits 为例）

舍入（四舍五入）

既然浮点数的表示这么奇怪，那如果我把两个浮点数相加，是不是可能得到不精确的结果？真聪明，确实如此！我们一般采取“round-to-even”的策略，即先考虑舍入到更近的那个数，如果两个数一样近，把得到的结果向着更“偶数”的方向去舍入，对二进制表示来说，就是希望它被舍入到结尾为 0 的那个数上.

来个例子：

10.000112 10.002 (<1/2—down) 10.001102 10.012 (>1/2—up)
10.111002 11.002 ( 1/2—up)
10.101002 10.102 ( 1/2—down)

主要好处是减少统计偏差。如果我们采取 round up，在统计时统计出的值可能偏高；如果选择 round down，统计出的值可能偏低。

加法，乘法

浮点数的加法和乘法性质并不良好，我直接把课件复制过来吧：

浮点数加法：

1. 封闭性：是
   • 但可能生成无穷大(infinity)或非数值(NaN)
2. 交换律：是
   • a + b = b + a
3. 结合律：否
   • 由于溢出和舍入的不精确性
   • 例如：(3.14+1e10)-1e10 = 0，而 3.14+(1e10-1e10) = 3.14
4. 零元素：是
   • 0 是加法单位元
5. 逆元素：几乎是
   • 除了无穷大和 NaN 外，每个元素都有加法逆元
6. 单调性：几乎是
   • a ≥ b ⇒ a+c ≥ b+c
   • 但对无穷大和 NaN 例外

浮点数乘法：

1. 封闭性：是
   • 但可能生成无穷大或 NaN
2. 乘法交换律：是
   • a × b = b × a
3. 乘法结合律：否
   • 由于溢出和舍入的不精确性
   • 例如：(1e20×1e20)×1e-20 = inf，而 1e20×(1e20×1e-20) = 1e20
4. 单位元：是
   • 1 是乘法单位元
5. 分配律：否
   • 由于溢出和舍入的不精确性
   • 例如：1e20×(1e20-1e20) = 0.0，而 1e20×1e20 - 1e20×1e20 = NaN
6. 单调性：几乎是
   • a ≥ b 且 c ≥ 0 ⇒ a×c ≥ b×c
   • 但对无穷大和 NaN 例外

类型转换

double/float → int：对浮点数（无论是单精度还是双精度）来说，把它们转换成 int 相当于 rounding toward zero，即舍去小数后面的部分。我觉得这应该主要是实现起来方便，我们在 datalab 里实现了这种转换。如果转换后超出了 int 的可表示范围，这种转换行为未定义（一般会设为 TMin，type minimum，能表示的最小值）。

int → float：根据 rounding mode 进行四舍五入，毕竟存在一些 float 不能表示的 int 值。

int → double：精确转换，毕竟 double 的 frac 有 52 个 bits，能够表示所有可能的 int 值。

杂项

大端法和小端法

多字节对象在内部存储的字节顺序表示上也有大端法和小端法之分，即最高有效字节在前面还是后面。比如把十六进制的 0x01234567 存储为 01 23 45 67 还是 67 45 23 01。

我们可以用下面的代码检查自己的机器使用的是大端法还是小端法。

#include <stdio.h>

int is_little_endian() {
    unsigned int x = 1;
    // 将整数的地址转换为字符指针，访问其第一个字节
    char *c = (char*) &x;
    // 如果第一个字节是1，则为小端；如果是0，则为大端
    return *c;
}

int main() {
    if (is_little_endian()) {
        printf("系统是小端(Little Endian)\n");
    } else {
        printf("系统是大端(Big Endian)\n");
    }
    return 0;
}