写在前面
Datalab 的难度很高。它的难度主要体现在技巧性上,这在整数部分尤其明显。整数部分至少有一半题目我花了一小时以上才做出来,相较而言,浮点数的题目虽然分类讨论起来更麻烦,但更为平易近人,每道我花了四十分钟左右。
如果有某道题做不出来,不建议一直死磕。我们可以换一道题或是离开屏幕散散心,我相信这会有帮助。
做完以后,感觉自己已经是位运算领域大神了!
整数部分
整数部分的技巧性很强,不建议在某道题上死磕,做不出来就换一道,以后再来。
bitXor
本题要求用 ‘~’ 和 ‘&’ 实现 ‘^’,简单列个关于 ‘^’ 的真值表:
| x | y | x^y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
关注 x^y 为 1 时 x 和 y 的取值,可以发现 x^y == ((~x) & y) | (x & (~y)),再用德摩根律把 | 换成 ~ 和 & 即可。
/*
* bitXor - x^y using only ~ and &
* Example: bitXor(4, 5) = 1
* Legal ops: ~ &
* Max ops: 14
* Rating: 1
*/
int bitXor(int x, int y)
{
/* x Xor y = ((~x) & y) | (x & (~y))
a | b = ~(~a & ~b)
*/
return ~(~(x & ~y) & ~(~x & y));
}tmin
这是熟知的结论,tmin = $-2^{31}$ = 1 << 31
/*
* tmin - return minimum two's complement integer
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 4
* Rating: 1
*/
int tmin(void)
{
/* use left shift to compute tmin */
return 1 << 31;
}isTmax
这种“判断 x 是否等于 y”的题目的做法有很多种:
- 创建一个 y,把 x 和 y 相减(x - y == x + ((~y) + 1)),然后判断结果是否为 0.
- 创建一个 y,return !(x^y)
我这里是直接构建了 -Tmax = 100…01,然后检查 x-Tmax 是否为 0.
/*
* isTmax - returns 1 if x is the maximum, two's complement number,
* and 0 otherwise
* Legal ops: ! ~ & ^ | +
* Max ops: 10
* Rating: 1
*/
int isTmax(int x)
{
/* create a '0' and use '!' */
return !(x + 1 + (1 << 31));
}allOddBits
这道题我想了很久。后来根据尝试性地构造了 1010…1010,然后试出了 (x & mask) ^ mask 的写法。大致的思路是,既然我们只在乎奇数位的值,就先用 & 把偶数位的值去掉,后来惊奇地发现再做个 ‘^’ 和 ‘!’ 就能得到结果了。
/*
* allOddBits - return 1 if all odd-numbered bits in word set to 1
* where bits are numbered from 0 (least significant) to 31 (most significant)
* Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 12
* Rating: 2
*/
int allOddBits(int x)
{
/* (x^y) == 0 <=> x == y */
int y = 0xAA; // 0xAA 就是二进制的 1010 1010
int mask = y + (y << 8) + (y << 16) + (y << 24);
return !((x & mask) ^ mask);
}negate
这是熟知的结果,本质是 $x + \sim x + 1 \equiv
0(\text{mod $2^{32}$})$
/*
* negate - return -x
* Example: negate(1) = -1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 5
* Rating: 2
*/
int negate(int x)
{
/* well known result */
return ~x + 1;
}isAsciiDigit
这道题我想了很久。后来分析了输入的形式,发现它只能形如 0000 … 0011 0yyy 或是 0000 … 0011 100y,于是决定把自由的位置右移掉,然后用 mask。
做完后复盘发现还有一种基于比较的方法,直接计算 x - 0x30 和 x - 0x39 并判断其符号位。
/*
* isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
* Example: isAsciiDigit(0x35) = 1.
* isAsciiDigit(0x3a) = 0.
* isAsciiDigit(0x05) = 0.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 15
* Rating: 3
*/
int isAsciiDigit(int x)
{
/* x 只能形如下面两种形式:
* 1. 0000 ... 0011 0yyy
* 2. 0000 ... 0011 100y
* 这里的 y 可以是 0 或 1
* 我们用右移去掉未知的 y, 然后用 mask即可
* 构造两个 mask, 一个是 0000 ... 0000 0110, 另一个是 0000 ... 0001 1100
*/
int mask1 = 0x06;
int mask2 = 0x1C;
return !((x >> 3) ^ mask1) | !((x >> 1) ^ mask2);
}conditional
这道题我也想了好久。一开始为了方便,我先用 !!x 把 x 归到了 0 或 1. 之后的思路是想构造满足类似 f(0, y) = 0,f(1, y) = y 的条件的函数 f,然后返回 f(x, y) + f(!x, z). 稍加思考,便发现 ‘&’ 和这里的 f 很像,于是就写下去了。
/*
* conditional - same as x ? y : z
* Example: conditional(2,4,5) = 4
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 16
* Rating: 3
*/
int conditional(int x, int y, int z)
{
/* 为了方便, 先限制 x 只取 0 或 1
* 我们一开始的思路是找到函数满足 f(x, b) = b if x == 1, 0 if x == 0
* 然后用 f(x, y) + f(!x, z) 即可得到结果
* 中途发现 11...1 & b = b, 0 & b = 0, 和我们希望的结果很像
* 于是就这么写了
*/
int mask = (~(!x)) + 1; // x为0时得到全1,x非0时得到0
return ((~mask) & y) + (mask & z);
}isLessOrEqual
好吧,这道题我还是想了很久,毕竟我在做之前对位运算几乎一无所知。这道题更多是分类讨论,分为 xy 同号和 xy 异号的两种情况就行,连溢出都不会有。
/*
* isLessOrEqual - if x <= y then return 1, else return 0
* Example: isLessOrEqual(4,5) = 1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 24
* Rating: 3
*/
int isLessOrEqual(int x, int y)
{
/* 若xy同号(最高位相同), return 1 if y - x >= 0 else 0
* 若xy异号, return 1 if y的二进制表示最高位为0 else 0
*/
int signX = x >> 31;
int signY = y >> 31;
int diffSign = (signX & !signY); // (异号且 y >= 0, x < 0) ? 1 : 0
int diff = y + (~x + 1); // y - x
int sameSign = (!(signX ^ signY)) & ((diff >> 31) + 1); // (同号且 y - x >= 0) ? 1 : 0
return diffSign | sameSign;
}logicalNeg
这道题是我感觉第二难的题目,我的核心思路是“非 0 的 x 的二进制表示中至少有一个 1”,于是我就构造了 11…1 即 -1 这个特殊值,并期盼它能给我一些有趣的结果。
对正数 x 来说,x + (-1) 的最高位必然是 0,这能把正数和 0 区分开来,因为 0 + (-1) 的最高位是 1.
但负数怎么办呢?负数要分类讨论,很麻烦。于是我就想取输入值的绝对值,然后用 abs + (-1) 来区分非 0 值和 0. 我这里的代码采用的是类似的思路,不过当时没想到怎么求 abs,就写得更复杂了一些。
后来复盘时发现非 0 值 x 一定满足 (x | (~x)) 的最高位为 1,用这个方法更简单。
/*
* logicalNeg - implement the ! operator, using all of
* the legal operators except !
* Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
* Legal ops: ~ & ^ | + << >>
* Max ops: 12
* Rating: 4
*/
int logicalNeg(int x)
{
/*
* 先思考怎么表示 'x非0', 注意到 x非0 <=> x的二进制表示中至少有一个1
* 考虑用 -1(它的二进制表示全是1) + x 来得到一些中间量
* 接下来分类讨论, 如果 x为0, 则 -1 + x = -1,
* 如果 x为正数, -1 + x 的二进制表示以 0 开头
* 如果 x为负数, 要分类讨论 Tmin的情况, 处理起来不方便
* 至此, 正数和 0 就能通过 (-1 + x) >> 31 区分开来了, 正数得到 0, 0 得到 -1
* 接下来把负数整合进来
* 考虑到负数的负是正数, 我们自然就会考虑把负数转化成正数,再用 | 或者 & 来连接
* ((((~0) + x) >> 31)) & ((((~0) + negtivex) >> 31)) 就能把正数和负数都变成0, 0变成 -1
* 再 & 1 就能得到 !x 了
* 代码里又进一步简化了一下结果, 不过核心思路还是"把负数和正数统一起来"
* 这里的 (((~0) + x) & ((~0) + negtivex)) 把 & 提前到了移位前,
* 直接 & 了二进制表示的最高位(之前的先 >> 再 & 是 & 了二进制表示的最低位)
*/
int negtivex = (~x) + 1;
return ((((((~0) + x) & ((~0) + negtivex)) >> 31)) & 1);
}howManyBits
这道题是我感觉最难的题目。首先我们画出这个函数的图像(留给读者作为练习),会发现它关于 -0.5 对称,这表明 x 和 -x-1 耗费的位数相同,接下来我们就只要考虑非负数就行了。
找到非负数的最小 bits 数倒是不难,稍微写几个非负数就能发现,只要找到它值为 1 的最高位数,设其为 k,k + 1 即为结果。
之后的难点就是,如何找到这个非负数的“值为 1 的最高位数”了。线性搜索显然是可行的,我们可以用 $\sum_{m=0}^{31}!!(x >> m)$ 来得到这个位数,然而这样做耗费的操作数超出了限制。既然线性耗费的操作数太多,那我们自然就会想到二分。
但怎么做二分呢?这里的代码更多是我试出来的,没有什么清晰的理论指导,我们直接看图吧。
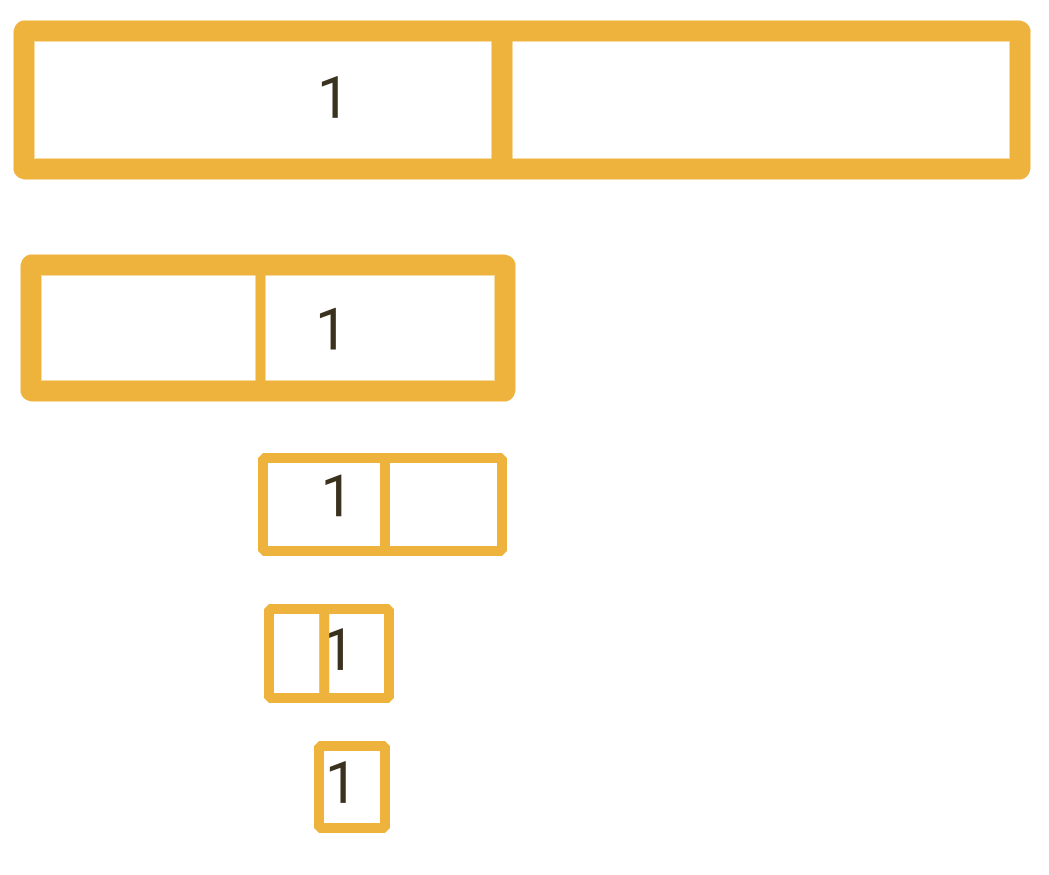
怎么做到“砍掉一半”呢?砍掉右边半段用右移就行,所以我们会从 x >> 16 开始,再用 !!(x >> 16) 是 0 还是 1 来判断 1 在右半边还是左半边。
之后的代码就真的纯粹是试出来的了,我们肯定能在数学上解释我们的操作,但具体的构思纯粹是试错+直觉试出来的,没什么好说的。
/* howManyBits - return the minimum number of bits required to represent x in
* two's complement
* Examples: howManyBits(12) = 5
* howManyBits(298) = 10
* howManyBits(-5) = 4
* howManyBits(0) = 1
* howManyBits(-1) = 1
* howManyBits(0x80000000) = 32
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 90
* Rating: 4
*/
int howManyBits(int x)
{
/* 简单画下这个函数的图像, 注意到 x 与 -x - 1(即~x) 耗费位数相同, 那就先统一转换成非负数,
* 然后找到最高的值为1的位数, 设其为 k, k + 1 即为结果
* 比如 0000 ... 0010 0110 的结果为 6 + 1 = 7
*
* 那怎么找到最高的值为1的位数呢?
* 一种想法是 sum([!!(alternatex >> k) for k in range(32)]), 但这样用的操作就超过限制了
* 所以我们借助二分的思想
* 让我们举个例子, 假设我们在处理 0010 1101,
* 我们可以先把它右移4, 发现仍然大于0, 就令ans += 4, 此时值为 0010 (扔掉右半部分)
* 然后右移2, 发现等于0, 则不在数据上真正移动, 值为 10 (扔掉左半部分)
* 再右移1, 发现大于0, 令 ans += 1, 此时值为 1 (扔掉右半部分)
* 当前的值不为0, ans +=1 (ans之前加了"被移除的部分的长度", 这里还要加上"剩余的部分的长度")
* 综上, 0010 1101 的最高的值为1的位数为6
*
* 首先我们要能够检查右移后值是否为0, 用!!(x >> k) 即可, !!(x >> k) == (x 右移后值为0) ? 0 : 1
* 然后为了方便在值上进行移动, 我们希望有 f(x) = (x 右移后值为0) ? 0 : 右移长度
* 因此使用形如 !!(x >> (2**k)) << k 的东西
*/
int signX = x >> 31; // (x >= 0) ? 00...0 : 11...1
int alternatex = ((~(signX)) & x) + ((signX) & (~x)); // (x >= 0) ? x : -x-1
int bit16 = (!!(alternatex >> 16)) << 4; // (alternatex >= 2**16) ? 16 : 0
alternatex = alternatex >> bit16;
int bit8 = (!!(alternatex >> 8)) << 3;
alternatex = alternatex >> bit8;
int bit4 = (!!(alternatex >> 4)) << 2;
alternatex = alternatex >> bit4;
int bit2 = (!!(alternatex >> 2)) << 1;
alternatex = alternatex >> bit2;
int bit1 = (!!(alternatex >> 1));
alternatex = alternatex >> bit1;
int bit0 = (!!alternatex);
return bit16 + bit8 + bit4 + bit2 + bit1 + bit0 + 1;
}浮点数部分
浮点数部分比起整数部分简单得多,只要仔细地分类讨论就行了。
floatScale2
分类讨论即可。这里比较有趣的是 exp == 0(denormalized case)的情况,无论 frac 部分是否超过 23 位,处理的代码都是一样的。
/*
* floatScale2 - Return bit-level equivalent of expression 2*f for
* floating point argument f.
* Both the argument and result are passed as unsigned int's, but
* they are to be interpreted as the bit-level representation of
* single-precision floating point values.
* When argument is NaN, return argument
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
unsigned floatScale2(unsigned uf)
{
/* 取出 exp 的部分, 分三种情况讨论.
* 1. NaN or infin, 直接返回输入值
* 2. denormalized case, 主要修改 frac 部分, 如果修改导致 frac
* 部分多于 23 位, 还要修改 exp 部分
* 3. normalized case, 修改 exp 部分
*/
unsigned exp = (uf >> 23) & 0xFF; // 00...0 exp
// 如果 exp == 二进制(1111 1111), uf为 NaN 或 infin, 直接返回uf
if (exp == 0xFF)
{
return uf;
}
// 如果 exp == 0, 就是 denormalized case
else if (exp == 0)
{
unsigned frac = (uf << 9) >> 9; // 0 00000000 frac
// 如果 frac 部分最高值为1, 进位; 如果不为1, 把 frac 部分乘二即可
// 两种情况都能用下面的代码来表示
frac = frac << 1;
return ((uf >> 23) << 23) + frac; // (s exp 00...0) + (0 00000000 frac)
}
// normalized case
else
{
// exp不会溢出8位, 因为前面的 if 分支已经处理了 exp == 0xFF的情况
exp += 1;
unsigned expmask = (~0) ^ (0xFF << 23); // 1 00000000 11...1
return (uf & expmask) + (exp << 23);
}
}floatFloat2Int
同样是分类讨论。一开始我把 NaN、infin 单独写了一种情况处理,后面发现操作数太多超出了限制,于是把它和绝对值太大的情况统一了起来,毕竟它们的返回值一样。
这里要仔细考虑的是 Tmin 落入的分支,在我的代码里,Tmin 落入了第一个 if 分支。
/*
* floatFloat2Int - Return bit-level equivalent of expression (int) f
* for floating point argument f.
* Argument is passed as unsigned int, but
* it is to be interpreted as the bit-level representation of a
* single-precision floating point value.
* Anything out of range (including NaN and infinity) should return
* 0x80000000u.
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
#include <stdio.h>
int floatFloat2Int(unsigned uf)
{
int exp = (uf >> 23) & 0xFF; // 00...0 exp
unsigned frac = (uf << 9) >> 9; // 00...0 frac
// 绝对值太大的情况
// 注意 NaN, infin也在这种情况中, 此时 exp == 0xFF
// -2^(31) 也在这种情况中, 此时 exp == 127 + 31, frac == 0
if (exp >= 127 + 31)
{
return (1 << 31);
}
// 绝对值太小的情况
else if (exp < 127)
{
return 0;
}
// 绝对值位于 [0, 2^(31) - 1] 的情况
// 该分支中, 0 <= exp - 127 < 31
else
{
int e = exp - 127;
int abs;
frac += (1 << 23);
// 如果 e 足够大, 保留 frac 里的所有数字, 否则舍弃后几位数字
if (e >= 23)
{
abs = frac << (e - 23);
}
else
{
abs = frac >> (23 - e);
}
// 根据正负返回不同值
// positive case
if ((uf >> 31) == 0)
{
return abs;
}
// negative case
else
{
return (~abs) + 1;
}
}
}floatPower2
还是分类讨论,不多说了。
/*
* floatPower2 - Return bit-level equivalent of the expression 2.0^x
* (2.0 raised to the power x) for any 32-bit integer x.
*
* The unsigned value that is returned should have the identical bit
* representation as the single-precision floating-point number 2.0^x.
* If the result is too small to be represented as a denorm, return
* 0. If too large, return +INF.
*
* Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while
* Max ops: 30
* Rating: 4
*/
unsigned floatPower2(int x)
{
/* float 可以表示的 2的幂次的范围为 [2^(-149), 2^(127)],
* 其中 [2^(-149), 2^(-127)] 由 denormalized case 表示,
* [2^(-126), 2^(127)] 由 normalized case 表示
*/
if (x < -149)
{
return 0;
}
// denormalized case
else if (x <= -127)
{
return 1 << (x + 149); // 只处理 frac 部分
}
// normalized case
else if (x <= 127)
{
return (x + 127) << 23; // 只处理 exp 部分
}
else
{
return (0xFF << 23); // +INF
}
}